Glossaire de la séquence 2
Glossaire des principales notions de la séquence
Tri actuellement Par date de modification ascendant Trier chronologiquement: Par date de modification
expérience aéatoireEn Probabilités, une expérience aléatoire est une expérience renouvelable (en théorie si ce n'est en pratique), et qui, renouvelée dans des conditions identiques - pour autant que l'observateur puisse s'en assurer - ne donne pas forcément le même résultat à chaque renouvellement : une succession de lancers d'une même pièce parfaitement équilibrée - et ne pouvant retomber sur sa tranche...- est un exemple classique. |
EvènementEn théorie des probabilités, un événement lié à une expérience aléatoire est un ensemble dont les éléments sont des résultats possibles pour cette expérience ( c'est-à-dire un certain sous-ensemble de l'univers lié à l'expérience). Un événement étant souvent défini par une proposition, nous devons pouvoir dire, connaissant le résultat de l'expérience aléatoire, si l'événement a été réalisé ou pas au cours de cette expérience. |
Espace probabiliséUn espace de probabilité(s)1 ou espace probabilisé est construit à partir d'un espace probabilisable en le complétant par une mesure de probabilité : il permet la modélisation quantitative de l' expérience aléatoire étudiée en associant une probabilité numérique à tout événement lié à l'expérience. Formellement, c'est un triplet |
Probabilité conditionnelleLa notion de probabilité conditionnelle permet de tenir compte dans une prévision d'une information complémentaire. Par exemple, si je tire au hasard une carte d'un jeu, j'estime naturellement à une chance sur quatre la probabilité d'obtenir un cœur ; mais si j'aperçois un reflet rouge sur la table, je corrige mon estimation à une chance sur deux. Cette seconde estimation correspond à la probabilité d'obtenir un cœur sachant que la carte est rouge. Elle est conditionnée par la couleur de la carte ; donc, conditionnelle. |

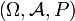 formé d'un
formé d'un 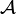 sur
sur