Il dépend de :

- la masse réduite μ du système A-B

- la constante de force de la liaison

Effet de k 

Fréquence de vibration proportionnelle à k

Effet de μ

   Fréquence de vibration inversement proportionnelle à μ

II.1.3 Energie de vibration

Pour décrire les forces agissant sur une liaison en vibration, on utilise l’énergie potentielle d’un oscillateur harmonique :

La courbe d’énergie potentielle en fonction de (r-r0) est une parabole.

II.1.4 Situation réélle des molécules

En réalité la forme du potentiel n’est pas rigoureusement parabolique mais suit la fonction de Morse :

Energie d'un oscillateur harmonique, modèle utilisé pour étudier les vibrations des molécules de type A-B

La courbe de l’énergie potentielle est  assimilée à la parabole de l’oscillateur harmonique pour des vibrations de faibles amplitudes.

a) Aspect quantique

Cas de l’approximation harmonique

   L’équation de Schrödinger selon la direction x :

Solution  : Ev = hν (v+1/2)

v : nombre quantique de vibration (v = 0, 1, 2..)

ν : fréquence de vibration (modèle classique)

Niveaux de vibration équidistants

   ΔEV = constante = hv

Les Liaisons ne sont pas des ressorts parfaits.

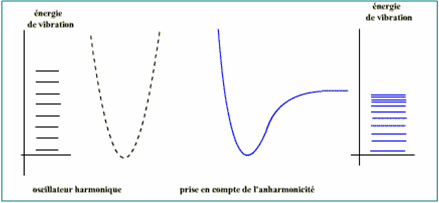
Les Niveaux de vibration de plus en plus rapprochés.

II.1.5 - Règles de sélection

Loi de Bohr hn = ΔE doit être vérifiée.

variation du moment dipolaire de la molécule

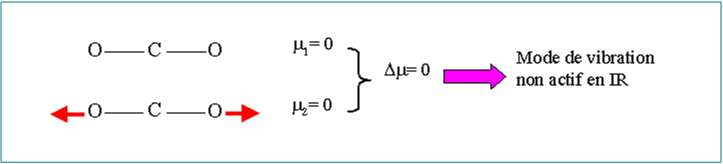
L’intensité absorbée est d’autant plus grande que la variation du moment dipolaire est grande.

II.1.6 Restriction quantique

Règle de sélection entre niveaux vibrationnels de nombres quantiques v : Δv = ± 1                                + : absorption                               -  : émission

Seul le niveau v=0 est significativement peuplé.

L'absorption observée résultera de la transition

v=0 → v=1.

II.1.7 - Rotation-vibration - Structure fine

Structure fine