Cours spectroscopie infrarouge
Analyser des données spectrales des molécules, interpréter des données infra rouges des molécules
| Site: | Touch By SukaJanda01 |
| Cours: | PC3513 : Chimie analytique et spectroscopie |
| Livre: | Cours spectroscopie infrarouge |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 17 juin 2025, 05:24 |
Table des matières
- 1 Spectroscopie Infrarouge
- 1.1 MICRO-ONDES
- 1.2 Equation des mouvements de rotation.
- 1.3 Les molécules en vibration
- 1.4 Les molécules en vibration suite1
- 1.5 Les molécules en vibration suite 2
- 1.6 Les molécules en vibration suite 3
- 1.7 Les molécules en vibrations suite
- 1.8 Etude structurale
- 1.9 Analyse structurale suite
- 1.10 Séquence vidéo pur L'IR
1 Spectroscopie Infrarouge
La liaison atomique est fondamentalement composée de charges électroniques, combinées dans un état stable. Selon la nature des atomes la liaison peut présenter un caractère de dipôle électrique si le centre de gravité des charges négatives, (les électrons de liaisons) est différent du centre de gravité des charges positives, (les noyaux). Ceci se produit de façon permanente quand les atomes liés ont des électronégativités différentes. La liaison est alors dite polaire. Cela ce produit aussi, mais de façon transitoire, notamment dans le cas de gros nuages électroniques, du fait des mouvements des électrons quand ils sont soumis à un champ électrique local intense. La liaison est alors dite polarisable.
1.1 MICRO-ONDES
I- Les micro-ondes
Dans ce domaine assez récent des ondes hertziennes ultra courtes, ( de l'ordre du centimètre). L'énergie des quanta est comparable à la différence entre deux niveaux de rotation des molécules.
Méthode expérimentale d'étude
Pour les molécules polaires, une variation du champ électrique exerce un couple sur le dipôle.
Si la fréquence propre de rotation de la molécule (domaine quantifié) correspond à la fréquence de radiation alors il y aura transfert d'énergie possible et donc une absorption. Si non, pour une molécule apolaire, où la somme des dipôles est nulle (CO2 linéaire ou de CCl4 symétrique) il n'y aura pas d'absorption. Les techniques utilisées diffèrent ici des techniques optiques, et elles ressemblent plutôt à celles de la production, propagation et détection des ondes radio et des ondes de télévision.
Les spectroscopies rotationnelles s’intéressent aux rotations des molécules sur elles-mêmes sans modification des positions relatives des atomes. Elles s’inscrivent dans le domaine d’énergie des micro-ondes, domaine plus récemment vulgarisé par les fours du même nom (mise en rotation des molécules d’eau).
Cette spectroscopie étudie les rotations des molécules autour de leurs différents axes d’inertie (axe de moindre inertie, axe de plus grande inertie). Des informations structurales peuvent être obtenues notamment concernant les longueurs de liaison et les angles de liaison, mais cette méthode n’est accessible qu’aux spécialistes et s’adresse en général à des molécules de petites tailles. La spectroscopie dans le domaine des micro-ondes et/ou d’ondes millimétriques est par ailleurs très utilisée dans la détection des molécules interstellaires à l’aide des radiotélescopes. La spectroscopie rotationnelle ne sera pas développée dans ce cours.
NB
Toutes ces variations d'énergie sont quantifiées et que la molécule n'absorbe pas une énergie quelconque. Elle n'absorbe que des énergies quantifiées.
En première approximation, on peut écrire que :
L'énergie totale Etotale = Erotation + Evibration + Eélectronique
Cependant ces trois termes ne sont pas rigoureusement indépendants les uns des autres. Les atomes sont en effet soumis à des formes centrifuges du fait de la rotation d'où un changement de l'énergie de rotation pour provoquer une variation de l'énergie de vibration ou de l'énergie électronique.
Lorsqu'une molécule passe d'un niveau d'énergie électronique ee à un autre niveau ee', elle passe du même coup d'un niveau d'énergie ev à ev' et également de er à e'r. Cette variation d'énergie de vibration, de rotation et électronique est de la forme :
1.2 Equation des mouvements de rotation.
1) Modèle du rotateur rigide.
a) Rotation d'une particule
On définit une fréquence de rotation vrot (nombre de tours effectués par seconde) et une vitesse angulaire notée ω.
Soit Ec = 1/2(mr2ω2) = 1/2(Iω2) avec I = mr2
b) Spectre d’absorption de rotation pure
Ce sont des spectres dans l’IR lointain. On utilise un rotateur
Cas des molécules diatomiques : le rotateur rigide
Soit la molécule diatomique A1A2 abandonnée à elle-même dans l’espace et soit G son centre de gravité. Il résulte les propriétés suivantes :
a) La quantité de mouvement totale de A1A2 est la même que si toute la masse est centrée en G.
b) En absence d’interaction extérieure, son centre de gravité est soit au repos soit animé d’un mouvement rectiligne uniforme.
c) Si A1A2 a un mouvement de rotation sur elle-même, celui-ci s’effectue autour d’un axe passant par son centre de gravité.
d) Si A1A2 a un mouvement de vibration le long de A1A2, il s’effectue en laissant G fixe.
Remarque
Le rotateur est supposé rigide c’est-à-dire que la distance d de A1A2 est constante (approximation)
c) Quelques définitions
La masse réduite du rotateur
Le moment d'inertie I du système par rapport à l'axe est
Pour ne molécule diatomique I = m1r12 + m2r22
Par ailleurs on a : m1r1 = m2r2 égalité des moments (propriété du centre de gravité)
Si on pose que r0 = r1 +r2 il vient que :
La masse réduite est le rapport du produit des masses sur la somme des masses et est notée m.
Le moment d'inertie du système est équivalent au moment d'inertie d'une masse réduite m placée à une distance invariable r0 du centre de gravité. Dans ce cas tout se passe comme si au lieu d'un mouvement de rotation de deux atomes A1 et A2 alignés avec G, il suffirait d’étudier autour de G celui de la masse réduite unique m située à une distance r0 de G. L’énergie mécanique de rotation de ce rotateur est :
ω la vitesse angulaire de rotation
d) Moment cinétique de rotation
Il est déterminé dans le cas d'une masse m tournant autour d'un point fixe.
On définit le moment cinétique par σ = μ.v.r avec v : la vitesse, r le rayon et μ la masse réduite
Condition de quantification : Energie de rotation
Ces conditions se portent sur le moment cinétique et s’expriment aussi bien sur un électron que sur un atome. Pour une période entière de mouvement, donc d’une rotation complète où l’angle j varie de 0 à 2π.
Avec j le nombre quantique de rotation qui ne doit prendre que des valeurs 0, 1, 2, 3 …… et que les règles de sélection identiques imposent que : Δj = ± 1
Exemples: le cas de HCl et CO
Remarque: On observe un spectre de rotation pure quand la molécule possède un moment dipolaire permanent. Si une molécule n’a pas de dipôle sa rotation ne peut engendrer un champ magnétique alternatif. Ainsi les molécules H2, N2, Cl2 …. Ne donnent pas de spectre en IR. Par contre HCl, HBr donnent des spectres.
Cas des molécules polyatomiques linéaires
La relation donnant les niveaux d'énergie de rotation possibles pour la molécule polyatomique linéaire est identique à celle correspondant aux molécules diatomiques.
Les niveaux d'énergie ont la même disposition que pour les molécules diatomiques mais ils sont plus rapprochés car le moment d'inertie est plus grand.
Exemple: H-12C=14N avec B = 1,48 cm-1 alors que pour HCl, B= 20,68 cm-1.
La sélection est encore ΔJ = ± 1 et comme les molécules diatomiques homonucléaires, les molécules symétrisues (CO2, C2H2) ne présentent pas de spectre de rotation pure.
Il est encore temps de considérer le cas où la molécule a au moins deux distances internucléaires. Dans ce cas on a pour une molécule de n atomes, n-1 liaisons. Comment déterminer à partir du spectre de rotation ces longueurs de liaison?
Exemple: cas d'une molécule triatomique linéaire.
Le moment d'inertie d'inertie d'une molécule polyatomique rigide par rapport à un axe donné est donné par la relation:
$$ \sum_{{i}={0}}^{n}m_{i} \cdot R_{i}^{2}$$
où mi est la masse de la particule i, située à la distance Ri de cet axe passant par le centre de gravité.
La solution du problème conduit au moment d'inertie I:
r1 et r2 sont les longueurs des deux liaisons de la molécule triatomique linéaire.
Les molécules polyatomiques non linéaires ou spatiales.
Une molécule linéaire ou spatiale possède trois moments d'inertie évoluant selon trois axes perpendiculaires appelés axes principaux. Ces moments sont notés IA, IB et IC. Ces molécules se divisent en trois catégories selon que leurs moments d'inertie possèdent une seule, deux ou trois valeurs différentes.
Les molécules de type sphérique
Les molécules dont les trois moments d'inertie sont égaux (IA = IB = IC) sont dites de type sphérique. Les moléculécules CH4 et SF6 ont des molécules sphériques.
Un traitement par la mécanique quantique des molécules sphérique s'apparente à celle des molécules diatomiques avec en plus de la constante B, l'introduction d'une autre constante appelée la constante de distorsion centrifuge D.
Cas des molécules de type toupie symétrique
Les molécules avec deux moments d'inertie égaux sont dites de type toupie symétrique.
Exemple: L'ammoniac (NH3), le chlorure de méthyle (CH3Cl), le pentachlorure de phosphore (PCl5), le pentafluorure de brome.
L'introduction de deux moments d'inertie distincts dans l'équation de Schrödinger conduit à la définition de deux nombres quantiques. Dans ce cas on garde le nombre quantique J et on ajoute un autre nombre quantique K qui prend les valeurs K = J, J-1, J-2, ...........,0, ......, -(J-1), -J.
L'énergie peut se mettre sous la forme:
Les règles de sélection applicables sont : ΔJ = ±1; ΔK = 0
1.3 Les molécules en vibration
Aperçu
Les molécules en mouvement de vibration ont absorbé une quantité d'énergie plus importante que celle qu'elles ont besoin pour la rotation.
Ev = hν(v+1/2),
Les mouvements des atomes d’une molécule peuvent être classés en trois catégories:
- les translations
- les rotations
- les vibrations
II- La spectroscopie vibrationnelle
II-1 Etude des vibrations moléculaires
Transitions dans la gamme 10-13000 cm-1
Les deux spectroscopies infrarouge (IR) et Raman étudient les vibrations des molécules lorsqu’elles sont irradiées par une onde électromagnétique de fréquence adéquate.
Le domaine de l’infrarouge se subdivise en trois régions :
Proche-IR 0,8-2,5 m 13300-4000 cm-1
IR moyen 2,5-25 m 4000-400 cm-1
IR-lointain 25-1000 m 400-10 cm-1
Sans l’infrarouge, l’énergie des photons modifie à la fois Erot et Evib
Molécule est équivalente à un rotateur-oscillant
1.4 Les molécules en vibration suite1
La rotation-vibration des molécules
III - ROTATION-VIBRATION DES MOLECULES DIATOMIQUES
III.1- La vibration
III.1.1- Energie de vibration
Les molécules ressemblent à un ensemble de boules : les atomes liées par des liaisons chimiques
Molécule soumise à une radiation infrarouge
Une molécule diatomique est formée de 2 atomes reliés entre eux par un ressort (liaison) telle est représentée par la figure ci-dessous.
Pour l'étude des vibrations moléculaires, on utilise le modèle de l'oscillateur harmonique
Oscillation décrite par une fonction sinusoïdale dont la fréquence ne dépend que des caractéristiques du système
L'oscillateur harmonique en mécanique classique
Soit un corps de masse m, fixé à l'extrémité d'un ressort de raideur k
Pour déplacer ce corps d'une distance x par rapport à sa position d'équilibre, on doit exercer une force qui engendre une force de rappel F.
Equation du mouvement
Solution générale de l'équation de Schrödinger est:
La force de gravitation fait que l'on peut introduire l'expression de l'énergie potentielle
Energie potentielle = f(élongation) conduisant à une parabole
III.1.2 Vibrations des molécules diatomiques - Approximation harmonique
a) Mécanique classique
Une molécule diatomique est équivaut à un oscillateur harmonique dont la liaison est un ressort de raideur k
|
|
masse µ (masse réduite) * constante de force k |
Fréquence de vibration dans l'approximation harmonique
En écartant les deux masses mA et mB d'une valeur (r-r0) par rapport à la distance d'équilibre r0. Puis le système est relâché à lui même, il se me à osciller.
Fréquence d'oscillation par la loi de Hooke
- ν : fréquence vibration - μ : masse réduite
- k : constante de force de la liaison
- mA et mB : masses des atomes A et B respectivement
La grandeur pratique en spectroscopie vibrationnelle est le nombre d'onde.
1.5 Les molécules en vibration suite 2
Il dépend de :
- la masse réduite μ du système A-B
- la constante de force de la liaison
Effet de k
Fréquence de vibration proportionnelle à k
Effet de μ
Fréquence de vibration inversement proportionnelle à μ
II.1.3 Energie de vibration
Pour décrire les forces agissant sur une liaison en vibration, on utilise l’énergie potentielle d’un oscillateur harmonique :
La courbe d’énergie potentielle en fonction de (r-r0) est une parabole.
II.1.4 Situation réélle des molécules
En réalité la forme du potentiel n’est pas rigoureusement parabolique mais suit la fonction de Morse :
Energie d'un oscillateur harmonique, modèle utilisé pour étudier les vibrations des molécules de type A-B
La courbe de l’énergie potentielle est assimilée à la parabole de l’oscillateur harmonique pour des vibrations de faibles amplitudes.
a) Aspect quantique
Cas de l’approximation harmonique
L’équation de Schrödinger selon la direction x :
Solution : Ev = hν (v+1/2)
v : nombre quantique de vibration (v = 0, 1, 2..)
ν : fréquence de vibration (modèle classique)
Niveaux de vibration équidistants
ΔEV = constante = hv
Les Liaisons ne sont pas des ressorts parfaits.
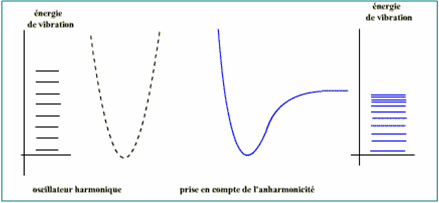
Les Niveaux de vibration de plus en plus rapprochés.
II.1.5 - Règles de sélection
Loi de Bohr hn = ΔE doit être vérifiée.
variation du moment dipolaire de la molécule
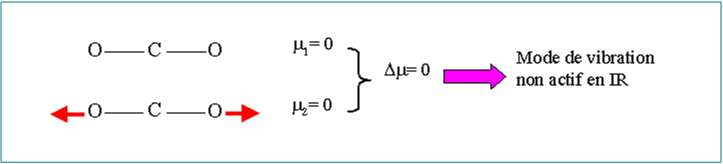
L’intensité absorbée est d’autant plus grande que la variation du moment dipolaire est grande.
II.1.6 Restriction quantique
Règle de sélection entre niveaux vibrationnels de nombres quantiques v : Δv = ± 1 + : absorption - : émission

Seul le niveau v=0 est significativement peuplé.
L'absorption observée résultera de la transition
v=0 → v=1.
II.1.7 - Rotation-vibration - Structure fine
Structure fine

1.6 Les molécules en vibration suite 3
En phase gazeuse : molécules tournent librement.
Région impliquée : IR-lointain (600-30 cm-1)
En première approximation
Les mouvements de rotation et de vibration sont indépendants :
rotateur rigide et oscillateur harmonique
Chaque mouvement garde ses caractéristiques :
niveaux d’énergie
nombres quantiques
règles de sélection
II.1.8 - Energie des molécules en rotation-vibration
E = Erotation + Evibration
Donc E = f (J,v) don l'expression est de la forme:
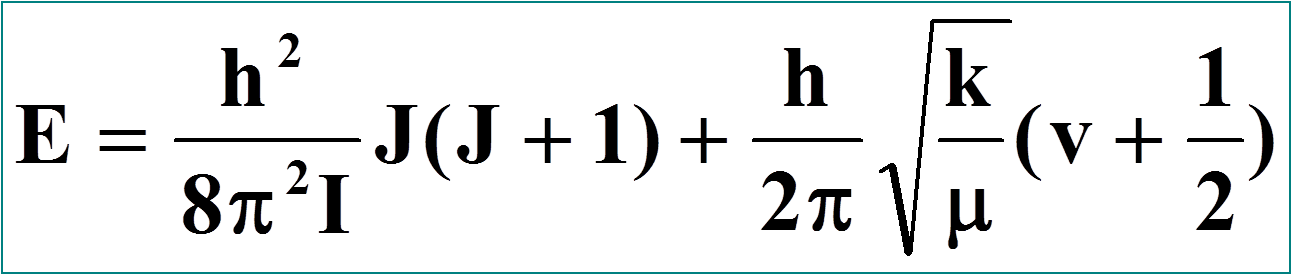
II.1.9 - Règles de sélection
Les conditions à satisfaire pour observer une transition en rotation-vibration :
- Le moment dipolaire permanent est variable au cours du mouvement avec des restrictions quantiques tellesque:
a) Δv = 0 : spectre de rotation pure
b) Δv = -1; ΔJ = ±1 : spectre d’émission
c) Δv = +1; ΔJ = ±1 : spectre d’absorption
| J →J’=J-1 : BRANCHE P J=0 →J’=0 : BRANCHE Q Vibration pure Transition interdite J → J’=J+1 : BRANCHE R |
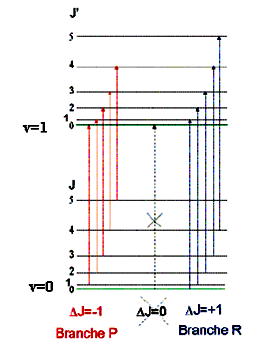 |
II.1.10 - Spectre de rotation-vibration
Les transitions de rotation-vibration conduisent à des séries de raies.
1.7 Les molécules en vibrations suite
Leurs intensités dépendent des populations des niveaux de rotation concernés (fonction de J).
II.2- VIBRATION DES MOLECULES POLYATOMIQUES
II.1 - Modes normaux de vibration
Molécule polyatomique est équivalente à des masses ponctuelles réunies ensemble par des ressorts.
II.1.1 Molécule de N atomes reçoit de l’énergie :
il en résulte un mouvement de vibration compliqué, décomposé en mouvements plus simples appelés
a) MODES NORMAUX DE VIBRATION
Nombre de modes normaux de vibration d'une molécule
Exemple: Les modes normaux de vibration de Al2Cl6
II.2 - Vibrations actives ou inactives - vibrations dégénérées
II.2.1 - Activité
Les mouvements de vibration ne sont pas tous actifs en infrarouge.
Vibration active en spectroscopie IR dépend de la variation du moment dipolaire
Exemple : La molécule de CO2

II.2.2 - La dégénérescence
Modes de doublement ou triplement dégénérés : Ce sont des modes ayant la même fréquence de vibration.
II.3 - Vibrations fondamentales
On appelle vibration fondamentale une vibration dont la fréquence correspond à celle d’un mode normal de vibration.
Théoriquement : (3n-6) ou (3n-5) vibrations fondamentales
Actives seulement si variation du moment dipolaire
II.3.1 Allure d’un spectre infrarouge
Spectre IR = Suite de bandes d’absorption, plus ou moins larges
Abscisse : en cm-1
Ordonnée : Transmittance (%T) ou Absorbance A = log(1/T)
Sur le spectre IR, on observe :
Certaines vibrations fondamentales sont absentes sur le spectre IR en raison de leur inactivité.
Mais d’autres bandes d'absorption apparaîssent.
Bandes de combinaison (ν1 + ν2 par exemple) : excitation simultanée de plusieurs vibrations fondamentales
II.3.2 - Types de mouvements de vibration et notations
En première approximation, les modes sont classés en fonction de deux paramètres :
Pour un groupement formé de plusieurs liaisons identiques :
II.3.3 les notations
Groupement fonctionnel formé d’une seule liaison (O-H, C=O..) :
δ : déformation dans les plan
γ : déformation hors du plan
Groupement formé de plusieurs liaisons identiques
II.4 - Les vibrations de groupe
Des groupes d’une molécule tels que (C=O, C-O, O-H, C-N, N-H, etc...) peuvent être excitées presque indépendamment du reste de la molécule.
Les bandes sont positionnées à des fréquences voisines sur les spectres IR et sont caractéristiques de ces fonctions.
Des tables permettent d'attribuer les absorptions aux différents groupes chimiques présents.
Région<1600 cm-1 : région des empreintes digitales.
III - APPLICATIONS DE LA SPECTROSCOPIE DE VIBRATION DANS L’INFRAROUGE
III.1 Composés organiques et inorganiques
Etat gazeux, liquide ou solide
Plusieurs grands champs d'application
III.2 - Analyse fonctionnelle
Détermination des groupements fonctionnels d’une molécule :
alcool, aldéhyde, cétone, acide...
Détermination des liaisons entre les carbones d'une chaîne :
chaîne saturée, insaturée, caractère aromatique d'une molécule...
Exemple : Liaisons C-H
Vibrations des liaisons C-H dépendent de l’hybridation de l'atome de carbone portant l'hydrogène.
Liaisons identiques dans un groupement
(ex. C-H d’un CH3 ou d’un CH2)
vibrent simultanément à la même fréquence.
Groupement CH2
Groupement CH3
1.8 Etude structurale
IV- Population thermique des niveaux de rotation ou intensité des pics d’absorption
Généralités :
L’intensité d’une raie spectrale dépend essentiellement des peuplements relatifs des deux états quantiques impliqués dans la transition.
Pour les spectres de rotation pure, les intensités relatives des raies dépendent des peuplements relatifs des états initiaux de chaque transition.
On peut calculer ces peuplements relatifs d’après la relation de Boltzmann.
Nj/Nj=0 = (2j+1)exp[(-hBcj(j+1)/KT] avec j = 0, 1, 2, 3, …….
Ce rapport est égal à (2j+1)exp[-ΔE/KT] où (2j+1) est le facteur de dégénérescence.
La valeur de j associée à la haute population peut être déterminée par dérivation du rapport de population en j. soit:
Le peuplement des états rotationnels ne doit pas décroitre de façon continue quand leur énergie augmente, c’est-à-dire que le diagramme du peuplement en fonction du nombre quantique j présente un maximum.
Les groupes fonctionnels donnent lieu à des absorptions infrarouges caractéristiques.
Les tables infrarouges donnent la liste des nombres d’ondes correspondant aux vibrations caractéristiques d’élongation de diverses liaisons de certains groupes fonctionnels de la chimie organique.
Il faut remarquer que la plupart des liaisons absorbent dans la région située au dessus de 1500 cm-1. Mais ces absorptions sont très similaires pour toutes les molécules organiques.
Un spectre d’absorption IR présente deux régions :
- Une région de vibration de valence de 1500 à 4000 cm-1.
- Une région de vibration de déformation de 1500 à 200 cm-1. Cette région est la plus intéressante car à chaque composé, il lui est assigné un spectre de déformation unique. Cette région est appelée la zone des empreintes digitales.
Exemple : les spectres de l’hexane et du pentane
En haute fréquence, les deux spectres sont typiques (au dessus de 1500 cm-1). Ce sont les vibrations d’élongation C-H des alcanes dans la région s’étendant de 2800 à 3000 cm-1.
Par contre, dans la fourchette 600 – 1500 cm-1 appelée la zone des empreintes digitales, les détails de leurs spectres diffèrent. Ces détails sont d’autant plus perceptibles que la sensibilité de l’enregistrement est grande.
Trois autres bandes apparaissent aux environs de 1460, 1380 et 730 cm-1.
Le spectre de l’hex-1-ène montre un trait caractéristique des alcènes par comparaison avec les alcanes est la présence d’une liaison Csp-H plus forte qui devrait se traduire par une bande plus énergétique dans le spectre IR. Cette bande est attendue à 3080 cm-1. Une autre bande d’élongation C=C devrait apparaître entre 1620 et 1680 cm-1 traduisant ce type de vibration.
Les autres bandes plus intenses résultent des mouvements de déformation angulaires. NB : Les deux bandes à 915 et 995 cm-1 sont typiques d’un alcène terminal.
La Liaison hydrogène
Liaison X-H, X = héteroatome (O, N, S)
Les liaisons hydrogène s'établissent entre deux hétéroatomes électronégatifs. Ces deux hétroatomes jouent le rôle de donneur et d'accepteur. Sur le spectre, la liaison hydrogène se manifeste par une grosse bande ν(OH).
Très fortes liaisons H existant entre O–H et C=O : dimères
En solution très diluée dans un solvant apolaire :
νOH est placée vers 3520 cm-1 (forme monomérique, OH libre)
Pour le carbonyle accepteur de liaison Hydrogène :
νC=O du monomère est vers 1760 cm-1
νC=O diminue de 40 à 60 cm-1 dans le dimère
IV.1 - Les effets inductifs et mésomères
IV.1.1 Cas d’une fonction carbonyle
- Cétone aliphatique : νC=O vers 1715 cm -1
IV.1.2- La conjugaison
Délocalisation d’une double liaison
diminution de la constante de force
diminution de la fréquence de vibration
Exemple : Le carbonyle conjugué, νC=O diminue de 15 à 40 cm-1
IV.1.3 - La tension de cycle
Oscillateur lié à une structure tendue stériquement sa fréquence de vibration augmente
IV.1.4 - Les isomères
1.9 Analyse structurale suite
D’autres modes de déformation angulaire donnant lieu à des absorptions intenses peuvent être mis à profit pour diagnostiquer le profil de substitution des alcènes.
- L’un traduit par une simple bande à 890 cm-1 et caractérise les 1,1-dialkyléthènes.
L’autre à 970 cm-1 plus aigue et reflète la vibration de déformation angulaire C-H d’un alcène en trans.
Il faut noter que l’absorption d’élongation O-H est la bande la plus caractéristique dans les spectres IR des alcools. Elle apparaît sous forme d’une intense et large dans la zone assez étendue (3200 – 3650 cm-1). La largeur de ce pic est due à des liaisons hydrogène avec d’autres molécules d’alcool ou avec de l’eau.
Les alcools anhydres et en solution donnent lieu à des bandes plus effilées dans une fourchette étroite (3620 – 3650 cm-1). Par contre, les liaisons C-X des halogénures présentent des fréquences d’élongation en IR à des énergies trop faibles (< 800 cm-1) pour présenter une utilité quant à leur caractérisation.
Un autre paramètre permettant d’identifier la structure d’une molécule : Le degré d’insaturation.
L’IR, ainsi que la RMN (Voir plus loin) constitue un outil de choix pour la détermination structurale d’un composé inconnu.
Quoi qu’il en soit, il existe, dissimilé dans la formule moléculaire de chaque composé, un élément supplémentaire d’information qui peut rendre la tâche plus aisée.
Ce nouveau paramètre est le degré d’insaturation qui est défini comme la somme des nombres de cycles et de liaisons π présents dans une molécule.
D’après ce tableau, on voit que chaque augmentation d’une unité dans le degré d’insaturation correspond à une perte ou diminution de deux hydrogènes dans la formule moléculaire.
C’est pourquoi, en se référant à la formule générale des alcanes acycliques (saturés : D.I. = 0) CnH2n+2, il est possible de déterminer le D.I. de n’importe que hydrocarbure en comparant tout simplement le nombre réel d’hydrogène qu’il possède à celui requis pour que ladite molécule soit saturée. Ce nombre correspond à 2n+2 avec n le nombre de carbone dans la molécule.
Exemple :
Quel est le degré d’insaturation de C5H8 ?
Réponse : Le composé saturé à 5 atomes de carbone est C5H2x5+2 = C5H12. Donc il manque à la molécule C5H8 quatre atomes d’hydrogène pour être saturée.
Donc le D.I. vaut alors 4/2 = 2.
NB : La présence d’hétéroatomes peut fausser le calcul.
Exemple : Comparons les formules moléculaires de quelques composés saturés.
L’éthane C2H6, l’éthanol C2H6O, ils ont le même nombre d’atomes d’hydrogène.
Le chloroéthane C2H5Cl possède un hydrogène de moins, tandis que l’éthanamine C2H7N en possède un de plus.
Le nombre d’atomes d’hydrogène correspond à la saturation est diminué en présence d’un halogène, augmente en présence d’azote mais n’est pas modifié par la présence de l’oxygène.
On peut généraliser le procédé de détermination du degré d’insaturation comme suit :
Etape1
Déterminer le nombre d’atomes d’hydrogène nécessaire pour que la molécule soit saturée, Hsat à partir du nombre de carbone (nC), d’halogène (nX) et d’azote (nN) qui sont présents dans la formule moléculaire.
Hsat = 2nC+2 –nX +nN
On ne tient pas compte de l’oxygène ni du soufre.
Etape 2
Déterminer le D.I. en comparant Hsat au nombre réel d’hydrogène présents dans la formule moléculaire, soit Hréel.
Résumé
Le degré d’insaturation est égal à la somme des nombres de cycles et de liaisons π dans une molécule. Le calcul de ce paramètre permet d’élucider plus facilement les structures à partir des données spectroscopiques.