5.4.1. Présentation

Les héliostats sont constitués d’un ou plusieurs miroirs réfléchissants plans ou légèrement concaves dont les surfaces sont comprises entre 50 m² et 150 m². Ils sont utilisés dans la technologie des tours solaires. Les miroirs sont montés sur une structure mécanique asservie à la trajectoire du soleil.

Figure 9 : Photo d’un héliostat de la centrale solaire de Themis

La monture la plus utilisée est la monture altazimutale mais il faut signaler aussi la monture rotation élevation (Non Focusing Imaging heliostat)  développée par les malaysiens qui restent à l'état de prototype.

5.4.2. Réflexion d'un héliostat vers un point fixe

Les rayons réfléchis par un champ d’héliostats doivent être dirigés vers le récepteur (tour centrale). Les angles de suivi et d’incidence de l’héliostat peuvent être déterminés à partir de la méthode des vecteurs.

Le repère cartésien basé sur les directions Zénith, Est et Nord avec l’origine O à la base du récepteur (O, z, e, n) voir figure 10. La position de l’héliostat  B est repérée par ses coordonnées z₁, e₁ and n₁. Le récepteur est situé à une hauteur z₀ de l’origine.

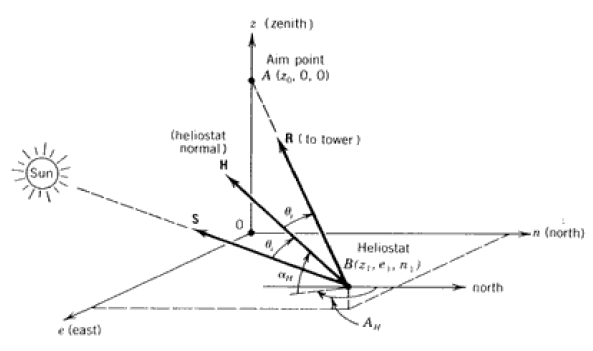
Figure 10: Coordonnées montrant la réflexion d’un rayon solaire par un héliostat vers un point fixe.

Pour déterminer la hauteur α_H et l’azimuth A_H de l’héliostat, nous utilisons trois vecteurs :

S : vecteur unitaire indiquant la direction du soleil

N : vecteur unitaire normal à la surface de l’héliostat

R : vecteur unitaire dirigé vers le point cible du récepteur, défini par :

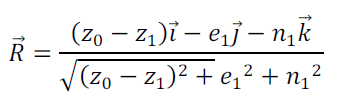        (26)

i, j, k vecteurs unitaires des directions z, e, n.

D’où

      (27)

Le vecteur normal H à la surface est définie par :

      (28)

D’après les lois de Descartes, l’angle d’incidence est égal à l’angle de réflexion.

L’angle d’incidence peut être décrit par les vecteurs S et N tels que :

         (29)

En combinant les équations (3.9) et (29), on a :

     (30)

Le vecteur normal N est la somme des vecteurs S et R, divisé par leur produit scalaire :

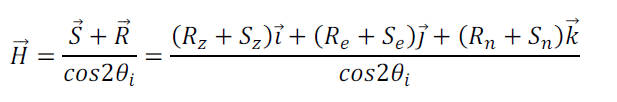      (31)

En remplaçant l’équation (3.9) et en décrivant la hauteur α_H et l’azimuth A_H de l’héliostat en termes de coordonnées d’une manière identique à celle représentée à la figure (3.6), on a :

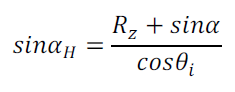           (32)

et

    (33)

La troisième expression est déterminée en complément:

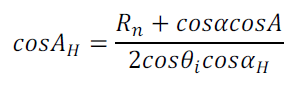     (34)