Chapitre 4: Capteurs solaires à concentration
Description
| Site: | Touch By SukaJanda01 |
| Cours: | Captation (Année 2015) |
| Livre: | Chapitre 4: Capteurs solaires à concentration |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 17 juin 2025, 19:35 |
Table des matières
1 Introduction
Les systèmes solaires thermodynamiques à transforment l'énergie rayonnée par le soleil en chaleur à température élevée, puis celle-ci en énergie mécanique (et électrique) à travers un cycle thermodynamique. Ils reposent essentiellement sur deux éléments majeurs que sont le capteur à concentration et le générateur d’énergie motrice. Le présent chapitre porte sur les capteurs à concentration.
2 .Généralités sur les capteurs à concentration
Elles portent sur le principe de fonctionnement et la classification des capteurs à concentration.
2.1 . Principe de fonctionnement
Les capteurs à concentration comme tout capteur thermique est un dispositif destiné à absorber le rayonnement solaire et à transmettre la chaleur ainsi produite à un fluide caloporteur. Dans ces systèmes à concentration, le rayonnement solaire est reçu par une surface d’ouverture et dirigé vers un absorbeur de surface plus petite grâce à une ou plusieurs réflexions, ou à des réfractions. Comparativement aux capteurs plans, les capteurs à concentration présentent de nombreux avantages:
-des températures opérationnelles élevées (de 100°C à 2000°C)
-des rendements plus élevés
-une réduction de la surface de l’absorbeur limite les pertes par convection
Ils présentent aussi des inconvénients :
-ces capteurs ne concentrent que le rayonnement direct
-ils nécessitent un système de suivi.
2.2 . Classification des capteurs à concentration
Il existe plusieurs types de concentrateurs et ils continuent de susciter l’intérêt des chercheurs. Plusieurs critères peuvent être utilisés pour distinguer les différents concentrateurs :
- les caractéristiques optiques permettent de différencier les systèmes imageants et les systèmes non imageants. Les concentrateurs imageants peuvent être linéaires ou ponctuels.
- le rapport de concentration C détermine les températures opératoires. On peut distinguer:
-les faibles concentrations (1<C<10, T~150°C)
-les moyennes concentrations (10<C<100, T~300°C)
-les fortes concentrations (C>100 ; T>500°C)
- les caractéristiques géométriques. Nous distinguons :
-les systèmes à deux dimensions
-les systèmes à trois dimensions
- les modes de pointage. Les concentrateurs peuvent être :
-fixes ou périodiquement orientés
-mobiles autour d’un axe
-mobiles autour de deux axes
- les positions relatives de l’absorbeur et du concentrateur selon que l’un est mobile par rapport à l’autre ou que les deux sont solidaires.
2.3 Rendement des capteurs à concentration
D'une manière générale, le rendement d'un capteur à concentration est
(1)
Aa: surface d'ouverture du capteur
Ib,n: rayonnement direct
θi: angle d'incidence
Tout: Température de sortie du fluide
Tin: Température d'entrée du fluide
![]() : Débit massique du fluide
: Débit massique du fluide
3 . Géométrie parabolique
Elle décrit l'équation d'une parabole, la surface cylindro-parabolique et celle d'une paraboloïde.
3.1 . Parabole
La parabole est définie comme une courbe plane dont chacun des points est situé à égale distance d'un point fixe, le foyer F, et d'une droite fixe, la directrice D. Notons que FR est égale à RD. La droite perpendiculaire à la directrice et passant par le foyer F est appelé axe de la parabole. Le sommet de l parabole, situé sur l’axe est à mi-distance entre le foyer F et la directrice D.
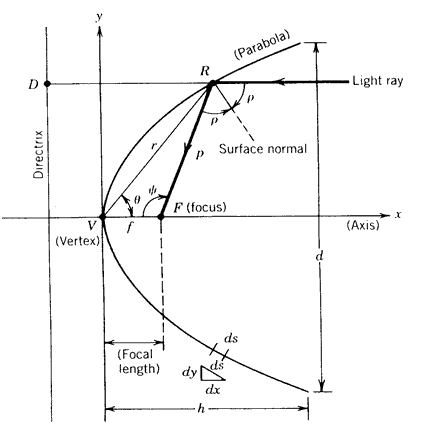
Figure 1 : Parabole
- Lorsque l'origine du repère est confondu avec le sommet de la parabole et (x'x) est l'axe de la parabole, l'équation de la parabole s'écrit en coordonnées cartésiennes:
![]() (2)
(2)
distance focale f=VF.
- En coordonnées polaires où r est le rayon, le sommet de la parabole est confondu avec l’origine du repère et symétrique par rapport à l’axe (x'x).
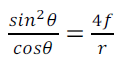 (3)
(3)
En pratique, la parabole est étudiée en coordonnées polaires en choisissant l’origine du repère au foyer F et en fonction d’un angle Ψ mesuré entre la droite (VF) et le rayon p de la parabole, on a :
![]() (4)
(4)
Souvent utilisée comme concentrateur, la parabole a la propriété de faire converger tous les rayons parallèles au foyer. On peut monter que:
![]() (5)
(5)
En energie solaire, les paraboles utilisées ont des limites, par conséquent, la parabole peut être décrite en fonction de l'angle d'ouverture'' rim angle'' et du rapport entre la distance focale et le diamètre d’ouverture (f/d), voir figure 2.
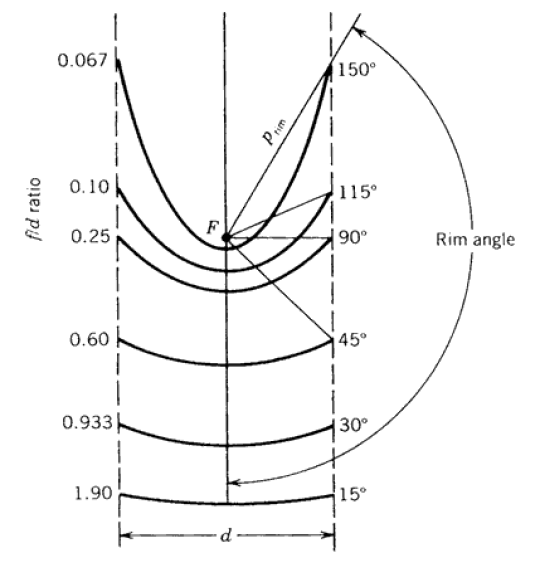
Figure 2: Segments de parabole ayant le même foyer et le même diamètre d'ouverture
La hauteur h peut être définie comme la distance maximale du sommet de la parabole à une droite tracée à travers l’ouverture:
 (6)
(6)
L'angle d'ouverture peut être déterminé à partir des dimensions de la parabole:
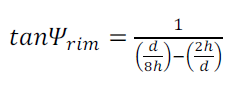 (7)
(7)
La longueur de l'arc s de la parabole peut être déterminée pour le cas particulier défini par pour x = h et y = d/2 en intégrant l'équation (1):
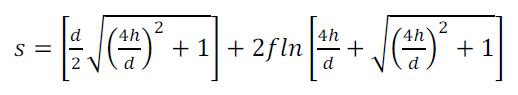 (8)
(8)
d est le diamètre d’ouverture de la parabole et h est la distance du sommet à l’ouverture.
3.2 Surface cylindro-parabolique
Les surfaces cylindro-paraboliques concentrent le rayonnement sur une ligne lorsque le plan contenant les axes de la parabole est aligné parallèlement aux rayons du soleil.
- Pour une surface cylindro-parabolique de longueur l et ayant des dimensions en coupe transversale représentées sur la figure 1, la surface d’ouverture est :
![]() (9)
(9)
- La surface réfléchissante est déterminée en utilisant la longueur de l’arc développée dans l’équation (7):
![]() (10)
(10)
La distance focale f et l'angle d'ouverture Ψ d’une surface cylindro-parabolique sont déterminées à partir des équations (5) et (6).
3.3 . Paraboloïde
3.3.1. Définition
Le paraboloïde est la surface obtenue par révolution d'une parabole autour de son axe. Les concentrateurs ayant cette surface sont appelés concentrateurs paraboliques ‘’Dish’’.
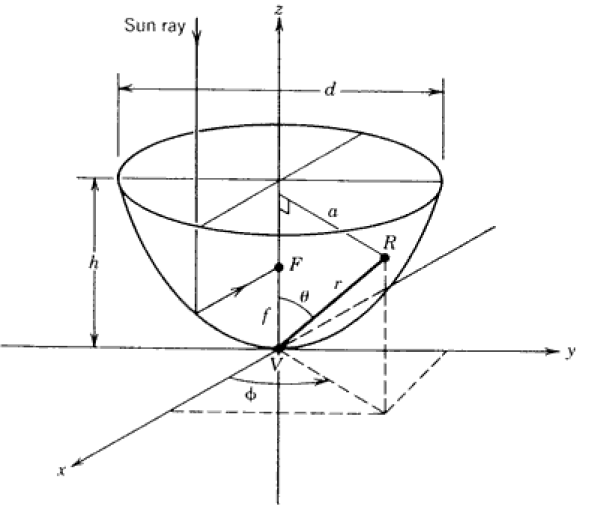
Figure 3: Paraboloïde
3.3.2. Equation de la paraboloïde
L’équation d’un paraboloïde d’axe de symétrie z en coordonnées cartésiennes est :
![]() (11)
(11)
Distance focale f=VF
- En coordonnées cylindriques, l’équation de la paraboloïde est :
 (12)
(12)
a: distance à l'axe.
- En coordonnées sphériques, où l’origine du repère est confondu avec le sommet de la paraboloïde, l'équation est:
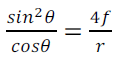 (13)
(13)
chaque point de la paraboloïde est repéré par les coordonnées (r, θ, Φ).
3.3.3. Surfaces de la paraboloïde
-La surface totale du paraboloïde peut être déterminée en intégrant l’équation (12). Définissons une surface élémentaire ds telle que:
![]() (14)
(14)
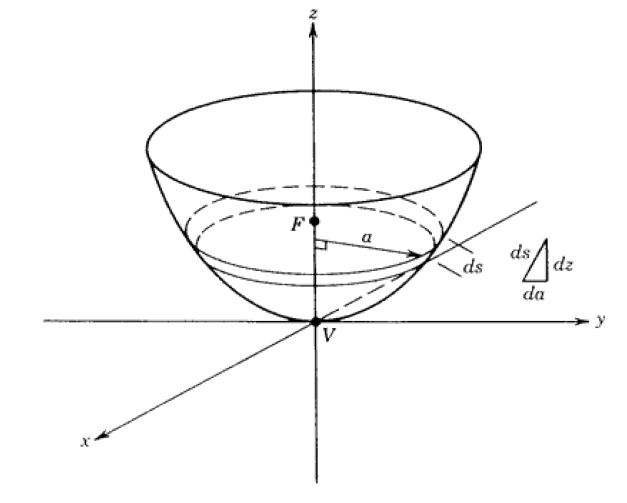
Figure 4: : Elément de surface d’un paraboloïde
En remplaçant dz, on a :
![]() (15)
(15)
La surface totale du paraboloïde de distance focale f et de diamètre d’ouverture d s’obtient en intégrant l’équation (13), on a :
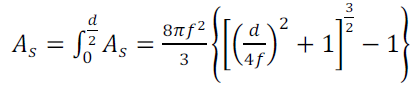 (16)
(16)
La surface d’ouverture est la zone circulaire qui s’appuie sur le diamètre d’ouverture d :
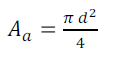 (17)
(17)
La surface d’ouverture peut être exprimée en fonction de la distance focale f et de l’angle d’ouverture Ψ. En utilisant l’équation (4), nous avons:
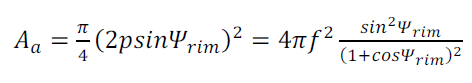 (18)
(18)
4 . La concentration
Cette partie porte sur l'ouverture du concentrateur, la concentration géométrique et les limites de la concentration.
4.1 . Ouverture du concentrateur
Le concentrateur est le dispositif optique qui permet de concentrer le rayonnement vers l’absorbeur. L’ouverture du concentrateur est la surface plane qui s’appuie sur ses bords et à travers laquelle passe le rayonnement incident. Pour un concentrateur cylindrique, l’ouverture est caractérisée par la largeur tandis que pour une parabole, elle est caractérisée par le diamètre d’ouverture.
4.2 . La concentration géométrique C
La concentration géométrique est le rapport de la surface d’ouverture Aa à celle de l’absorbeur Ar.
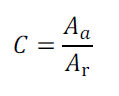 (19)
(19)
4.3 . Les limites de la concentration
La concentration ne peut dépasser une valeur limite appelée concentration idéale. Cette notion fut introduite par Winston et reprise par Rabl.la concentration limite est différente selon que le système est à deux dimensions (concentrateurs linéaires) ou à trois dimensions (paraboloïde).
La concentration limite est basée sur le second principe appliqué à l’échange radiatif entre le soleil et un récepteur.
Considérons un système à trois dimensions de surface d’ouverture Aa et de récepteur Ar regardant le soleil de rayon r à la distance R.
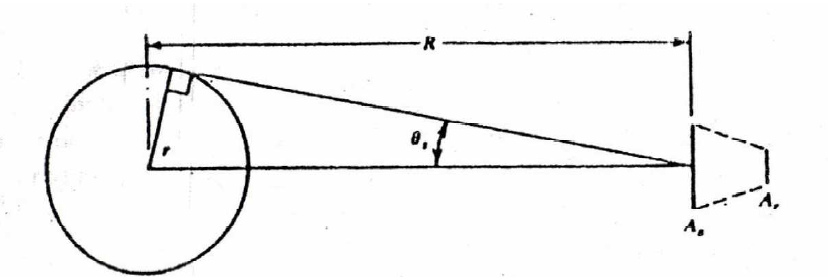
Figure 5: Schéma du soleil à la température Ts à la distance R d’un capteur à concentration de surface d’ouverture Aa et de récepteur Ar
Le flux rayonné par le soleil et intercepté par la surface d’ouverture Aa:
 (20)
(20)
Un récepteur parfait considéré comme un corps noir rayonne une énergie égale à ![]() et une fraction
et une fraction ![]() atteint le soleil:
atteint le soleil:
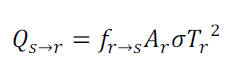 (21)
(21)
En vertu du second principe de la thermodynamique, il ne peut y avoir échange d’énergie entre deux corps à la même température. Donc si :
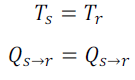 (22)
(22)
Ce qui entraine:
 (23)
(23)
Lorsque ![]() tend vers 1, le maximum de concentration est :
tend vers 1, le maximum de concentration est :
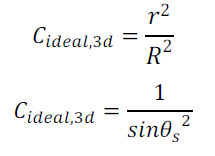 (24)
(24)
Un raisonnement analogue pour les systèmes à deux dimensions (concentrateurs linéaires) conduit à :
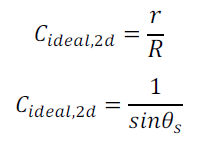 (25)
(25)
diamètre apparent du soleil: Θs=16'.
5 .Types de concentrateurs
Il se répartissent en concentrateurs cylindro-paraboliques, en réflecteurs linéaires de Fresnel (LFR), en concentrateurs paraboliques, en héliostats et en concentrateurs paraboliques composés.
5.1 . Les capteurs cylindro-paraboliques
La surface réfléchissante du concentrateur est un cylindre de section parabolique. Lorsqu’ils sont bien orientés vers le soleil, ils concentrent le rayonnement direct sur une ligne focale ou se trouve le récepteur (figure 6). Le mécanisme de poursuite du soleil se fait suivant un seul axe. Les concentrateurs cylindro-paraboliques peuvent être orientés suivant l’axe Est-Ouest ou l’axe Nord-Sud. Les concentrateurs orientés suivant l’axe Nord-Sud permettent de collecter plus d’énergie pendant l’été . L’orientation Est-Ouest permet une collecte d’énergie généralement supérieure . Les températures de travail varient de 270°C à 450°C et les rendements de conversion de ces capteurs sont voisins de 70% en régime nominal. Dans la pratique, les angles d'ouverture sont inférieurs à 20-30°. C’est la technologie la utilisée dans les centrales thermodynamiques.

Figure 6: capteurs cylindro-paraboliques
5.2 . Les capteurs à réflecteurs linéaires de Fresnel (LFR)
Ils sont constitués de miroirs plans ou faiblement paraboliques disposés en lames parallèles qui sont susceptibles d’être inclinés sur un axe de manière à réfléchir et à concentrer les rayons lumineux vers une ligne ou se trouve le récepteur (figure 7). Comparativement aux PTC, les LFR sont plus faciles à fabriquer, le système de suivi utilise des moteurs plus petits, la ligne focale est fixe, le montage du champ solaire est facilité et mieux utilisé (70% du sol peut être couvert de miroirs) [11]. La performance optique des LFR est diminuée de 30 à 40% par rapport aux PTC.

Figure 7 : Concentrateur à réflecteur linéaire de Fresnel
5.3 . Les capteurs paraboliques
Ils sont des concentrateurs ponctuels ayant une symétrie de révolution parabolique. Les rayons solaires réfléchis par la parabole convergent vers le foyer (figure 1-5). Ils sont orientés grâce à des montures mobiles autour de deux axes (monture altazimutale et monture équatoriale). La nécessité de mobiliser la parabole suivant deux axes pour suivre la course du soleil est la limite principale de ce type de système. Le concentrateur parabolique couplé avec un moteur sterling (Dish-Stirling) est la technologie la plus utilisée pour la production d’électricité de faible puissance par conversion solaire thermodynamique. Les rendements des capteurs sont voisins de 75 %, les puissances des installations correspondent à la gamme 1-100 kWth, les taux de concentration de 6000 à 10000 permettent d’obtenir des températures de travail de 600°C à 1200°C. Le rendement instantané de conversion énergie solaire-électricité est supérieur à 22% (29 % pour le module de 25 kW du constructeur américain SES (Stirling Energy Systems)) mais les coûts d’exploitation et de maintenance restent élevés.
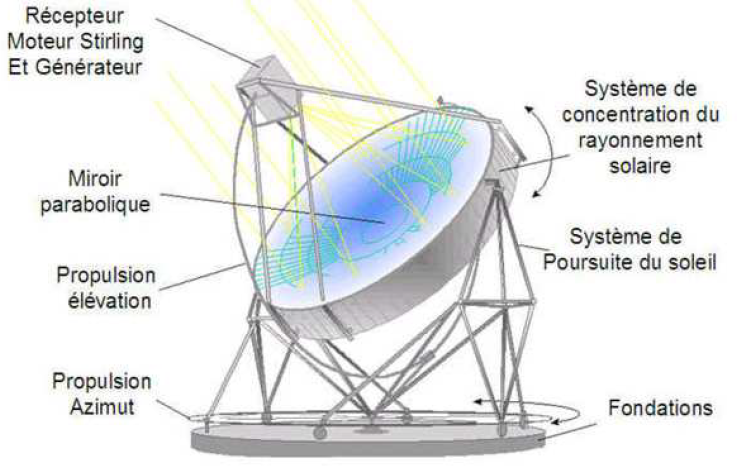
Figure 9 : Concentrateur parabolique avec un moteur Stirling
5.4 . Les héliostats
5.4.1. Présentation
Les héliostats sont constitués d’un ou plusieurs miroirs réfléchissants plans ou légèrement concaves dont les surfaces sont comprises entre 50 m2 et 150 m2. Ils sont utilisés dans la technologie des tours solaires. Les miroirs sont montés sur une structure mécanique asservie à la trajectoire du soleil.

Figure 9 : Photo d’un héliostat de la centrale solaire de Themis
La monture la plus utilisée est la monture altazimutale mais il faut signaler aussi la monture rotation élevation (Non Focusing Imaging heliostat) développée par les malaysiens qui restent à l'état de prototype.
5.4.2. Réflexion d'un héliostat vers un point fixe
Les rayons réfléchis par un champ d’héliostats doivent être dirigés vers le récepteur (tour centrale). Les angles de suivi et d’incidence de l’héliostat peuvent être déterminés à partir de la méthode des vecteurs.
Le repère cartésien basé sur les directions Zénith, Est et Nord avec l’origine O à la base du récepteur (O, z, e, n) voir figure 10. La position de l’héliostat B est repérée par ses coordonnées z1, e1 and n1. Le récepteur est situé à une hauteur z0 de l’origine.
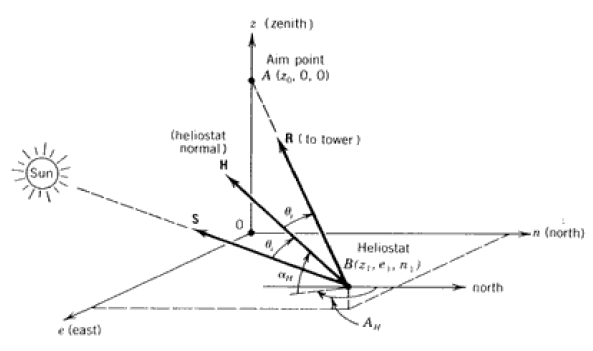
Figure 10: Coordonnées montrant la réflexion d’un rayon solaire par un héliostat vers un point fixe.
Pour déterminer la hauteur αH et l’azimuth AH de l’héliostat, nous utilisons trois vecteurs :
S : vecteur unitaire indiquant la direction du soleil
N : vecteur unitaire normal à la surface de l’héliostat
R : vecteur unitaire dirigé vers le point cible du récepteur, défini par :
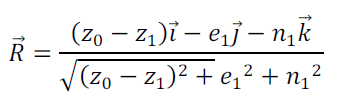 (26)
(26)
i, j, k vecteurs unitaires des directions z, e, n.
D’où
![]() (27)
(27)
Le vecteur normal H à la surface est définie par :
![]() (28)
(28)
D’après les lois de Descartes, l’angle d’incidence est égal à l’angle de réflexion.
L’angle d’incidence peut être décrit par les vecteurs S et N tels que :
![]() (29)
(29)
En combinant les équations (3.9) et (29), on a :
![]() (30)
(30)
Le vecteur normal N est la somme des vecteurs S et R, divisé par leur produit scalaire :
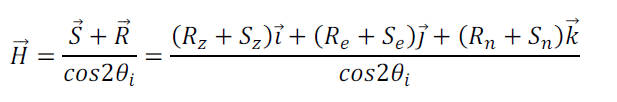 (31)
(31)
En remplaçant l’équation (3.9) et en décrivant la hauteur αH et l’azimuth AH de l’héliostat en termes de coordonnées d’une manière identique à celle représentée à la figure (3.6), on a :
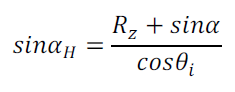 (32)
(32)
et
 (33)
(33)
La troisième expression est déterminée en complément:
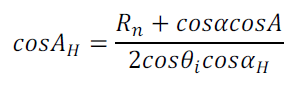 (34)
(34)
5.5 . Les concentrateurs paraboliques composés
Les concentrateurs paraboliques composés (CPC) ne forment pas d’image du soleil. Ils sont particulièrement intéressants dans les systèmes à deux dimensions. Sous sa forme la plus simple, un CPC à absorbeur plan est composé de deux arcs de parabole symétriques.
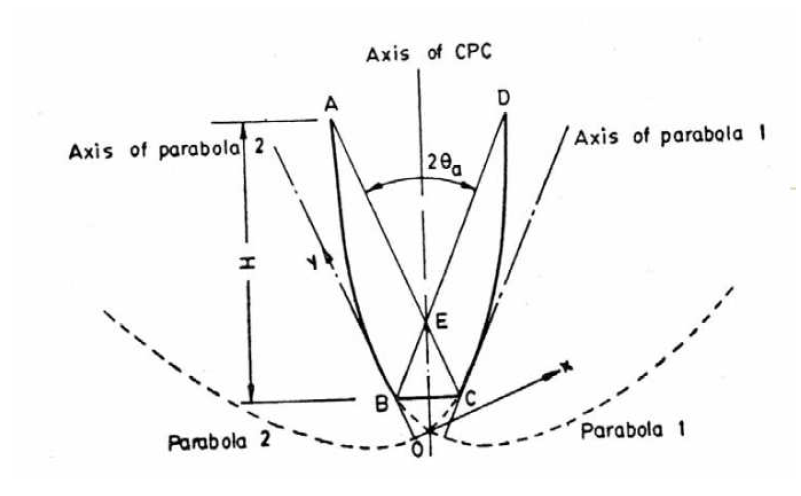
Figure 11: Concentrateur parabolique composé
La concentration maximale d’un CPC est:
![]() (35)
(35)
Si les CPC permettent d’atteindre la concentration idéale, ils présentent par contre l’inconvénient de nécessiter à concentration égale et pour un même absorbeur, une surface de miroirs plus importante.
Mais il est possible de réduire la surface des miroirs sans trop nuire aux performances du concentrateur. Il suffit pour cela de supprimer la partie supérieure du CPC. En effet, cette zone intervient peu dans le rayonnement car le rayonnement incident y est presque parallèle au miroir.
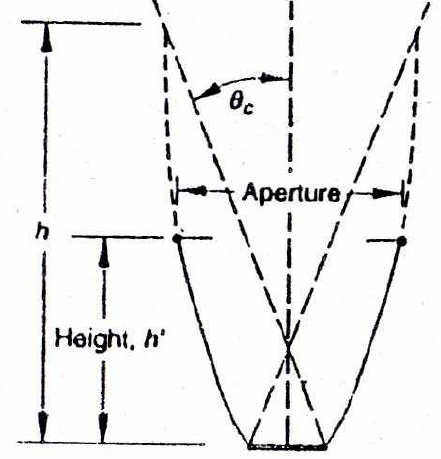
Figure 12: Concentrateur parabolique composé tronqué