2.1.1. Angle de suivi et angle d'incidence

Un système de suivi fait tourner le capteur à concentration autour d’un axe de rotation jusqu’à ce que le rayonnement solaire et la normale au capteur soit coplanaire.

La figure suivante illustre une surface d’ouverture en mouvement de rotation autour d’un axe en vue de suivre le soleil.

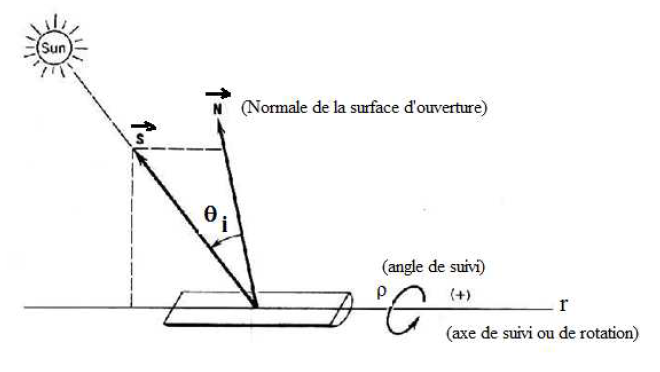
Figure 3 : Surface d’ouverture en rotation autour de l’axe r

S est dans le plan formé par r et N

θ_i : angle d’incidence

ρ : angle de suivi défini par  lorsque N est vertical

Pour déterminer les angles θ_i  et ρ en fonction des coordonnées du système horizontal, nous adoptons le système de coordonnées (u,b,r) dont r est le vecteur unitaire d’un des axes du système et u vecteur unitaire de l’axe vertical.

N tourne toujours dans le plan u,b.

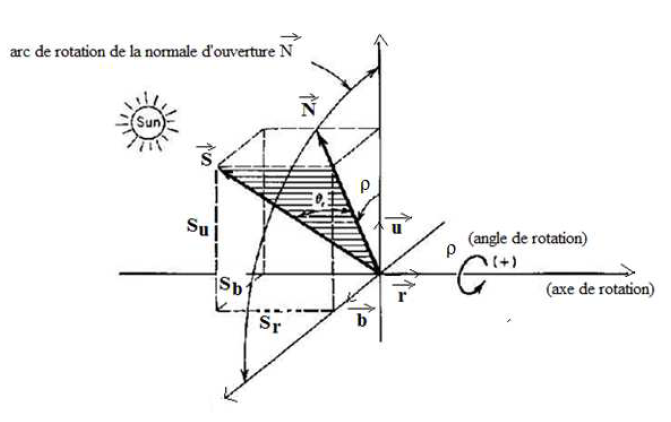
Figure 4 : Système de coordonnées avec un seul axe de suivi r

On a :

Pour l’angle de suivi :

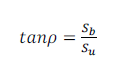        (8)

S est un vecteur unitaire, sa projection sur le plan r-b nous permet de déterminer le cosinus de l’angle d’incidence

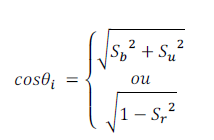                    (9)

2.1.2. Axe de suivi horizontal

Pour décrire les différents schémas de suivi, nous utilisons le passage du système d’axes (u,b,r) système d’axes (z,e,n) par rotation autour de l’axe z.

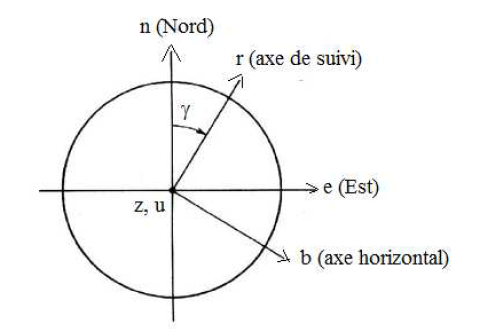
Figure 5 : Passage du système d’axes (u,b,r) au système d’axes (z,e,n) par rotation autour de l’axe z

On a la matrice de rotation suivante :

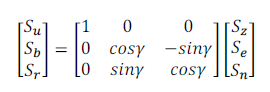                   (10)

Par développement et en remplaçant, on a les formules générales de l’angle de suivi et du cosinus de l’angle d’incidence tel que :

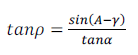                      (11)

et

                    (12)

Ces formules peuvent être simplifiées pour les cas suivants :

• Axe de suivi orienté dans la direction Nord-Sud 

      (13)

et

         (14)

• Axe de suivi orienté dans la direction Est-Ouest

              (15)

et

            (16)

2.1.3. Axe de suivi incliné

L’axe de suivi est incliné arbitrairement d’un angle β par rapport à l’horizon

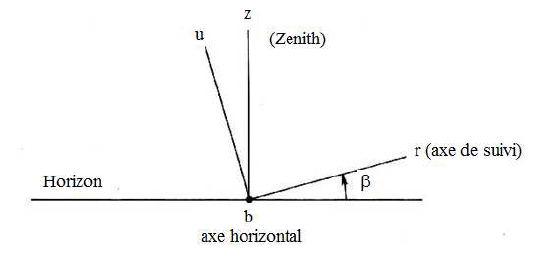
Figure 6 : Rotation des coordonnées du capteur autour de l’axe horizontal b

On a :

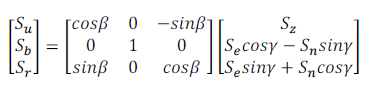      (17)

En développant les équations on obtient

          (18)

et

(19)

Ces équations se simplifient lorsque le capteur est incliné face Sud en posant

γ=180°

2.1.4. Décalage de la surface d’ouverture

Dans certains cas de figure, la surface d’ouverture est décalée d’un angle μ.

L’angle de suivi est déterminé à partir de l’équation (18) lorsque N demeure dans le plan formé par S et N. L’angle d’incidence devient la somme de l’angle d’incidence calculée dans l’équation (19) et de μ.

μ est positif lorsque le décalage se fait dans le sens trigonométrique autour de l’axe b.

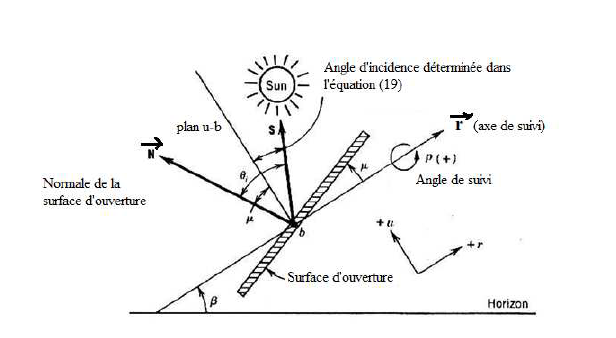
Figure 7: Surface d’ouverture décalée avec suivi suivant l’axe r

Particulièrement pour les équations (18) et (19), deux cas pratiques ont lieu:

-capteur disposé verticalement

-capteur dont l'angle de suivi est incliné à la latitude du lieu

2.1.4. Quelques cas de suivi habituels

• Axe de suivi vertical

Lorsque l'axe de suivi est colinéaire à l’axe du zenith, on a:

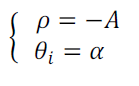                           (20)

Par convention l’angle de suivi est compté positivement dans le sens trigonométrique.

• Axe de suivi vertical avec une surface d’ouverture décalée

La surface d’ouverture est décalée d’un angle μ par rapport à l’axe vertical de rotation

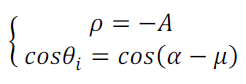                  (21)

μ=0, lorsque l’axe de suivi est dans le plan de la surface d’ouverture du capteur.

• Axe de suivi incliné à la latitude du lieu

Lorsque l’axe de suivi est incliné d’un angle égal à la latitude du lieu, l’axe de rotation devient parallèle à l’axe des pôles. On a:

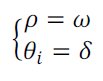                           (22)

Toutefois, l’angle horaire  varie de 15° par heure, un simple système à horloge peut permettre de faire le suivi.