Chapitre 1: Description et caractérisation du rayonnement solaire
INTRODUCTION
| Site: | Touch By SukaJanda01 |
| Cours: | Captation (Année 2015) |
| Livre: | Chapitre 1: Description et caractérisation du rayonnement solaire |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 1 juillet 2025, 03:20 |
Table des matières
1 .Introduction
Le soleil est la source d’énergie la plus importante et la plus commune. Cette source abondante d’énergie peut être utilisée dans les systèmes thermiques ou photovoltaïques. Son exploitation s’effectue à partir de données obtenus auprès des services météorologiques cependant une grande inégalité règne pour les données disponibles selon les potentialités économiques du pays concerné. Ce chapitre est consacré à l’estimation du rayonnement solaire au sol.
2 .Coordonnées géographiques
Un point à la surface de la terre est repéré par deux coordonnées angulaires : la latitude et la longitude .
2.1 .Longitude λ
La longitude λ d’un lieu correspond à l’angle que fait le plan méridien passant par ce lieu avec un plan méridien retenu comme origine. On choisit pour méridien origine (0 °) le plan passant par l’observatoire de Greenwich. Par convention on affecte du signe (+) les méridiens situés à l’est de ce méridien et(‐) les méridiens situés à l’ouest.
2.2 .Latitude ϕ
La latitude ϕ d’un lieu correspond à l’angle avec le plan équatorial que fait le rayon joignant le centre de la terre à ce lieu. L’équateur terrestre est donc caractérisé par une latitude égale à 0 °, le pôle nord par la latitude +90 °et le pôle sud par la latitude ‐90 °. Cette convention de signe affecte le signe (+) à tous les lieux de l’hémisphère nord et le signe (‐) tous les lieux de l’hémisphère sud.
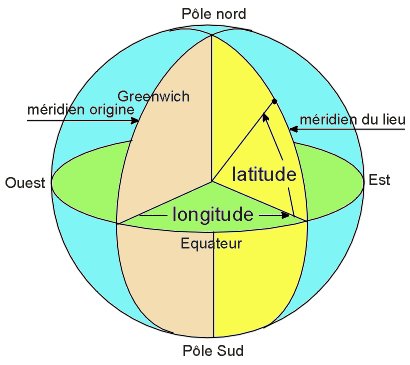
Figure 1 : Longitude et latitude d’un lieu
-Comment repérer les coordonnées géographiques d'un lieu?
N.B: poster les réponses dans le forum
3 .Temps solaire
Le calcul de la position du soleil, nécessaire au calcul des éclairements implique une bonne connaissance de l’instant de calcul.
3.1 Temps sidéral
Le temps sidéral est défini par rapport aux étoiles. Le jour sidéral correspond à la période de rotation de la terre sur elle-même. C'est le temps qui sépare deux passages consécutifs d'une étoile au méridien du lieu d'observation.
3.2 . Temps solaire moyen TSM
Ce temps est défini par rapport à un soleil fictif autour duquel la terre se déplace à vitesse constante et qui passe chaque année, au même instant que le soleil réel au point vernal (intersection de l’écliptique et de l’équateur céleste). La journée solaire moyenne est donc constante (24 H). Son origine est midi comme tous les temps sidéraux.
3.3 . Equation du temps ET
L’écart entre le TSV et le TSM est appelé équation du temps. En effet, la variation de la vitesse de la terre sur sa trajectoire autour du soleil introduit un terme correctif appelé équation du temps noté :
ET s’exprime en min
3.4 . Temps universel
C’est le temps solaire moyen du méridien de Greenwich pris comme origine. La terre est alors divisée en 24 fuseaux horaires de 15° de longitude chacun, numérotés en heures vers l’Est de 0 à 23 et correspond à des décalages d’une heure par rapport au méridien O.
4 . La sphère céleste
La sphère céleste est une sphère imaginaire de rayon gigantesque avec la terre située en son centre. Les pôles de la sphère céleste sont alignés avec les pôles de la Terre. Elle permet de représenter tous les astres (ici le soleil) tels qu’on les voit depuis la terre.
Figure : Sphère celeste
5 .Système de coordonnées horaires
Il sert pour viser un astre en un lieu donné. Les éléments de référence sont le demi-méridien Sud du lieu d’observation (plan vertical passant par le pôle Nord) et le plan de l’équateur. Ces deux plans sont fixes par rapport à l’observateur et permettent ainsi un repérage local. La direction d’un astre est alors caractérisée par deux angles: l’angle horaire et la déclinaison.
5.1 . Angle horaire
Pour décrire la rotation de la terre autour de son axe polaire, nous utilisons le concept de d’angle horaire. Comme illustré à la figure 2, l'angle horaire est la distance angulaire entre le méridien de l'observateur et le méridien dont le plan contient le soleil. Cette mesure se fait à partir du Sud en tournant vers l'Ouest.
Figure: Angle horaire
Elle s'exprime le plus souvent en heures, minutes et secondes, mais parfois aussi en degrés (de 0° à 360°, dans le sens rétrograde).
5.2 .Déclinaison
Elle représente l’angle formé entre la direction du soleil et le plan équatorial. Elle varie tout au long de l’année.
Figure: Déclinaison
Sa loi de variation en degré s’écrit:
6 . Système de coordonnées horizontales
Le système de coordonnées horizontales constitue le système de coordonnées locales le plus utilisés. Les éléments de référence sont : le plan horizontal du lieu, et le demi-méridien Sud du lieu d’observation. Dans ce système de coordonnées, la direction d’un astre est caractérisé par son azimut A et sa hauteur h.
6.1 .Hauteur du soleil α
C’est l'angle qui sépare l'astre du plan horizontal voir figure 5. Comme alternative l'altitude du soleil peut être décrite en termes de l'angle solaire zénithal θz qui est tout simplement le complément de l'angle d'altitude solaire
6.2 . Azimut A
C’est l’angle que fait la direction de la projection du soleil sur le plan horizontal avec la direction Nord, il est orienté dans le sens horaire.
Figure :
Système de coordonnées horizontales pour le vecteur position S repéré par les coordonnées a, θz et A
Remarque
Il existe d'autres conventions pour la mesure de l’azimut solaire en usage dans la littérature solaire. L'une des conventions les plus courantes consiste à mesurer l''azimut avec la direction Sud pointant plutôt que la direction Nord. Une autre est de considérer le sens trigonométrique plutôt que le sens horaire.
6.3 .Expressions de la hauteur et de l’azimut en fonction de la latitude, l’angle horaire et la déclinaison
Il est important pour la conception des capteurs solaires de calculer la hauteur du soleil et l’azimut à tout moment pour n’importe quel endroit de la terre. Cela est possible en utilisant la latitude φ, l’angle horaire ω et la déclinaison δ. Pour ce calcul, nous définissons le vecteur soleil (figure 6) tel que:
Par projection dans le repère (Q,i ,j , k ) on a :
De même, un vecteur soleil peut être décrit au centre de la terre, comme le montre la figure 6.
Figure 6: Système de coordonnées horaires pour le vecteur position soleil repéré par les coordonnées ω et δ
L’origine de ce système d’axes est le centre de la terre, l’axe m est défini par l’origine C et le point d’intersection entre le méridien d’observation et le plan équatorial, l’axe e perpendiculaire à l’axe m est situé dans le plan équatorial. L’axe p est aligné avec l’axe de rotation de la terre .
Par projection dans ce système d’axes, on a:
Ces deux systèmes de coordonnées sont liés par une rotation d’axe e, d’angle de latitude ϕ et de translation de rayon terrestre QC. Nous négligeons la translation le long du rayon terrestre car c’est environ 1/23 525 de la distance de la Terre au Soleil, et donc la différence entre les vecteurs de direction S et S ' est négligeable.
Le passage du système d’axes (m ,e , p) au système d’axes (z , e, n) par rotation d’axe e est décrit à la figure 7:
Figure 7
Avec les matrices de passage par rotation, on a :
Figure 8 : Vue composite des figures 5, 6 et 7
En combinant les équations (4), (7) et (8) on obtient:
L’équation (10) est une expression de la hauteur solaire fonction de l’angle solaire (ω), de la déclinaison (δ) et de la latitude ( ). En résolvant nous aurons :
De même nous aurons deux méthodes de calcul de l'azimut solaire (A). Encore une fois, ces expressions sont données en tenant compte de la convention de signe utilisée dans notre texte, c'est-à-dire que l'angle de l’azimut solaire est mesuré à partir du nord dans le sens horaire. La résolution nous donne alors un programme suivant :
7 .Ombres solaires
Maintenant que nous avons développés les équations appropriées pour définir la direction du soleil sur n’importe quel jour, n’importe quand et n’importe où, nous allons examiner un point qui est intéressants et peuvent être utiles pour le concepteur.
Comme nous le savons la lumière du soleil voyage sur des lignes droites, ainsi la projection d’un point obscur sur le sol (ou sur toute autre surface) peut être décrite en termes géométriques simples. Le problème ici est de définir la longueur et la direction de l’ombre portée par le pole ; ce sera d’abord en coordonnées radiales puis en coordonnées cartésiennes.
En coordonnées radiales, pour une hauteur de mât OP et un azimut de l’ombre As définit de la même manière que les angles d’azimut antérieur c'est-à-dire par rapport au nord vrai (aiguille d’une montre étant positif), nous avons pour la longueur de l’ombre :
Et pour l’azimut de l’ombre :
En termes de coordonnées cartésiennes, avec la base du poteau comme origine, au Nord comme direction de y > 0 et à l’Est comme direction de x > 0, les équations pour les coordonnées de l’extrémité de l’ombre à la verticale OP des pôles sont :
Figure 9 : Ombre portée par le pôle OP donnée en coordonnées cartésiennes et l'azimut (As)
8 .Aspects énergétiques du rayonnement
Ce partie s'intéresse au rayonnement extraterrestre, à l'interaction rayonnement atmosphère et au rayonnement arrivant au sol.
8.1 . Rayonnement solaire extraterrestre
8.1.1. Constante solaire
Le soleil étant assimilé à un corps noir, à partir de la loi de Stefan-Boltzmann, on peut déterminer la température d’émission du soleil.
Le soleil rayonne dans toutes les directions avec:
Figure 10 : Eclairement reçu par une sphère de rayon intérieur
L’éclairement reçu par la sphère de rayon intérieur rSE est égal au flux rayonné par le soleil
Ceci permet de déterminer l’irradiance directe extraterrestre, toutefois la distance terre soleil n’étant pas constante durant l’année, l’irradiance extraterrestre varie entre 1325 W/m2 and 1420 W/m2. Sa valeur moyenne est appelée constante solaire Gsc
8.1.2. Rayonnement à la limite de l'atmosphère sur une surface normale
a. Mouvements de la terre
La terre décrit autour du soleil une orbite elliptique de faible excentricité, avec une période de 365,25 jours. Le plan de cette orbite est appelé plan de l’écliptique.
Figure 11 : Mouvement de la terre autour du soleil
La terre tourne sur elle-même sur une période sensiblement également à 24 h, qui se traduit par la succession des jours et des nuits. L’axe de rotation de la terre fait un angle de 23°27’ avec la normale du plan de l’écliptique.
b. Rayonnement
En raison de la variation terre-soleil, le rayonnement solaire à la limite de l’atmosphère varie. D’après Duffie et Beckmann, le rayonnement solaire à la limite de l’atmosphère sur une surface normale au rayonnement solaire est:
8.1.3.Rayonnement solaire extraterrrestre sur une surface horizontale
La figure 12 montre le rayonnement solaire sur une surface horizontale.
Figure 12:
Le rayonnement solaire sur une surface horizontale à un instant donné est
8.2 .Effets de l'atmosphère
8.2.1. L'atmosphère
L’atmosphère est l’enveloppe de gaz qui entoure la Terre. Son épaisseur est de 1500 km, les 50 premiers kilomètres contenant 99,9 % de son volume global. En fonction des variations que la température y subit, les météorologues partagent l'atmosphère en quatre couches à partir du sol qui sont :
- La troposphère ou basse atmosphère : riche en vapeur d'eau et en nuages, son épaisseur est d'une dizaine de kilomètres et la température y décroît régulièrement (en moyenne de + 15 °C à - 56 °C).
- La stratosphère ou moyenne atmosphère: jusqu'à une cinquantaine de kilomètres d'altitude. Les réactions photochimiques induites par la présence de l'ozone fournissent à l'air un apport de chaleur de sorte que la température augmente jusqu'à des températures proches du zéro.
- La mésosphère : épaisse d'une trentaine de kilomètres, la température décroît de nouveau jusqu'à - 90 °C.
- La thermosphère ou la haute atmosphère : des transformations physiques et chimiques affectent un air raréfié et soumis à des températures croissantes (jusqu’à + 500 °C à 500 km d’altitude).
8.2.2. Interaction entre l'atmosphère et le rayonnement solaire
A la traversée de l’atmosphère, le rayonnement solaire diminue du à son interaction avec l’atmosphère. La réduction du rayonnement solaire est due à
-la réflexion par l’atmosphère
-l’absorption dans l’atmosphère (due principalement aux gaz O3, H2O, O2 et CO2)
-la diffusion de Mie
-la diffusion de Rayleigh.
L’absorption du rayonnement solaire par les différents gaz de l’atmosphère est fortement sélective et influence quelques parties du spectre solaire. La figure 2 montre le spectre solaire hors atmosphère et sur terre. Le spectre solaire sur terre montre des baisses significatives pour certaines longueurs d’ondes dues à l’absorption.
Figure 14 : Spectres solaires extraterrestre et terrestre
Le degré d’atténuation du rayonnement solaire à travers l’atmosphère dépend du chemin optique et des caractéristiques du milieu traversé. Dans les calculs de rayonnement solaire, on utilise la notion de masse atmosphérique.
8.3 .Rayonnement solaire au sol
8.3.1. Indice de clarté
Les performances d’un système solaire doivent être testées à long terme. Par conséquent la connaissance des données relatives à la moyenne mensuelle de rayonnement solaire quotidien ainsi que de l’indice de clarté de la localité est exigée. Ces données sont éventuellement disponibles dans les services nationaux de météorologie ou dans les cartes.
La moyenne mensuelle de l’indice de clarté est définie par
8.3.2. Rayonnement solaire direct sur une surface normale au rayonnement solaire
a. Loi de Beer
Selon la loi de Bouguer-Lamber plus connu sous le nom de loi de Beer (circa 1760), L'atténuation de la lumière à travers un milieu est proportionnelle à la distance parcourue dans le milieu et le flux de rayonnement où k est un coefficient d’atténuation
b. Modèle basé sur le facteur de trouble de Linke
Plusieurs modèles de détermination du rayonnement direct basés sur le facteur de trouble de Link existent dans la littérature. La différence entre ces modèles réside dans l’approche du facteur et/ou dans la formulation du rayonnement solaire direct. Ce facteur sert à caractériser le trouble atmosphérique dû à la vapeur d’eau, à la brume, aux fumées, aux poussières, etc.
L’avantage de ces modèles est que les paramètres atténuant le rayonnement sont donnés en fonction d’un seul indice facile à utiliser. Pour ce modèle le rayonnement solaire direct est donné par :
Où α : hauteur solaire
TL : coefficient de trouble de Link
TL=2,5+16β+0,5ln(w)
β est le coefficient d’Angström qui exprime la quantité d’aérosol dans l’atmosphère, w est la hauteur d’eau des précipitations exprimée en cm.
c. Modèle de Yang
Ce modèle a été développé par Yang et al en 2001 pour déterminer le rayonnement direct. Il est déterminé à partir des coefficients d’atténuation de Raleigh, de l’ozone, de l’eau, des aérosols et des gaz. Le rayonnement direct est donné par :
τ r: : coefficient d’atténuation dû à la diffusion de Rayleigh
τg: coefficient de transmission après diffusion par les gaz
τ0: coefficient d’atténuation après absorption de l’ozone
Lat: latitude du lieu considéré et d: le nombre de jour
τw: coefficient d’atténuation après absorption par la vapeur d’eau
w: hauteur d’eau condensable en mm.
τa: coefficient de transmission après diffusion par les aérosols
e.Estimation du rayonnement solaire horaire à partir du rayonnement journalier
Elle donne de bons résultats pour des journées claires:
8.3.3. Rayonnement horaire dffus
On peut estimer le rayonnement horaire diffus en calculant le rayonnement global horaire et en utilisant la corrélation suivante:
8.3.4. Rayonnement global
Généralement les capteurs sont inclinés. Il est nécessaire de calculer le rayonnement solaire sur une surface d’orientation quelconque. Cette surface reçoit
-un rayonnement direct .
-un rayonnement diffus provenant de la voûte céleste .
-un rayonnement diffus réfléchi par le sol .
Figure 16 : Rayonnement direct sur surface horizontale et inclinée
9 .Dispositifs de mesure
Les rayonnements solaires sont mesurés à l’aide des radiomètres qui se retrouvent sous plusieurs formes selon le type de rayonnement étudié.
Le radiomètre qui permet de mesurer le rayonnement global est le pyranomètre. Et le rayonnement direct est mesuré par un pyrhéliomètre.

Figure: Dispositifs de mesure du rayonnement
Il existe aussi d’autres radiomètres qui mesurent d’autres grandeurs physiques, par exemple : Un héliographe, il permet d’enregistrer la durée d’insolation, période de la journée pendant lesquelles l’intensité du rayonnement direct a dépassé un certain seuil.