ANALYSE FINANCIERE DE PROJET
Consignes:
Ce document contient l'essentiel de ce qu'il faut lire pour réaliser les activités dans cette séquence du cours.
- Chaque étudiant est invité à le lire à se l'approprié avant de démarer les activités prévues.
| Site: | Touch By SukaJanda01 |
| Cours: | Gestion des Projets (Année 2015) |
| Livre: | ANALYSE FINANCIERE DE PROJET |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 17 juin 2025, 14:57 |
1 CHAPITRE II : ANALYSE FINANCIERE DE PROJET
CLASSEMENT DE L’INVESTISSEMENT RENTABLE
Les divers critères que nous avons étudiés permettent d’étudier la rentabilité d’un projet.
Un premier critère est ainsi établit entre investissement rentable et investissement non rentable.
Mais elle ne constitue qu’une première étape car les ressources de tout promoteur et de toute entreprise sont nécessairement limitées. Tous les investissements rentables ne pourront donc être sélectionnés à première vue. A première vue l’investissement qu’il faut sélectionner semble être celui qui à la VAN ou le TRI le plus élevé.
Cette stratégie n’est pas la seule envisageable.
Le critère de rentabilité maximal n’est pas toujours le seul critère pris en compte.
Par exemple un promoteur peut décider de rechercher l’investissement le plus utile, c'est-à-dire le plus conforme à ses intérêts défini au sens large.
1.1 CHOIX ENTRE DES PROJETS MUTUELLEMENT EXCLUSIFS
Il s’agit de porter un choix entre des projets qu’il n’est pas possible de réaliser ensemble, exemple construire une centrale électrique alimentée par du fuel ou une centrale électrique alimentée par du charbon.
1 - PROJETS DE MEME DUREE
Les critères de la VAN conduit à sélectionner celui des projets dont la VAN est plus grande.
|
Projet A |
Projet B |
|
I0 = 300 000 |
I0 = 400 000 |
|
CAFA = 100 000 |
CAFB = 130 000 |
|
Durée 5 ans |
Durée 5 ans |
CAF : capacité d’autofinancement
Coût du capital 15%

1.2 PROJETS DE DUREES DIFFERENTES
Comparons les deux projets suivants :
|
Projet A |
Projet B |
|
I0 = 150 000 |
I0 = 150 000 |
|
CAFA = 50 000 |
CAFB = 80 000 |
|
Durée 6 ans |
Durée 3 ans |
CAF : capacité d’autofinancement
Coût du capital 15%.
VANA = 39224
VANB = 32568
Selon le critère de la VAN, le projet A semble être préférable, mais cela ne tient pas compte du fait qu’après trois (3), il est possible de faire un autre projet B, de durée trois (3) ans qui augmentera la rentabilité du projet B.
Les projets de durée différente peuvent être comparés par l’une des trois (3) méthodes suivantes :
a) Renouvellement à l’identique du projet le plus court
Supposons que l’on peut faire un projet B’ de durée trois (3) ans après le projet B
|
Projet B et B’ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
I0 |
- 150000 |
|
|
- 150000 |
|
|
|
|
CAF |
|
80000 |
80000 |
80000 |
80000 |
80000 |
80000 |
![]()
VAN BB’ = 54131
VAN BB’ = 54131
VANA = 39224
VAN BB’ = 54131
VANBB’ > VANA Projet BB’ à sélectionner
La VAN des deux projets B consécutifs (durée totale 6 ans) étant supérieure à la VAN du projet A, le projet B sera préféré.
Cette méthode n’est applicable que dans le cas très particulier où la durée du projet long est un multiple de la durée du projet court.
b) Alignement sur la durée du projet le plus court
Raisonnons sur une durée de trois (3) ans pour les deux (2) projets A et B.
Il faudra évaluer ce que sera la valeur résiduelle des équipements du projet A à l’époque trois (3) :
- supposons que cette valeur résiduelle est à 70000
|
Projet A écourté |
0 |
1 |
2 |
3 |
|
I0 |
- 150000 |
|
|
- 150000 |
|
CAF |
|
50000 |
50000 |
50000
|
![]()
VANA = 10187
VANB = 32658
VANB > VANA Projet B à sélectionner
Cette méthode souffre de la difficulté d’évaluer les équipements en cours d’utilisation.
c) Méthode de l’annuité constante équivalente
Cette méthode consiste à calculer la somme qui est actualisée sur la durée de vie de l’investissement.
Et qui aurait permis d’obtenir la VAN issue de cet investissement.

La méthode de l’annuité constante est la meilleure des méthodes, elle est applicable en toutes circonstances.
1.3 CHOIX ENTRE PLUSIEURS PROJETS NON EXCLUSIFS EN CAS DE RATIONNEMENT DU CAPITAL
Les projets étudiés ne sont pas exclusifs l’un de l’autre. Tous les projets dont la VAN est positive pourraient être acceptés et appliqué si l’entreprise disposait d’un capital pour les financer en même temps.
On est cependant limité par l’insuffisance du capital.
Exemple :
Considérons une entreprise ou une division d’entreprise qui étudie de nombreux projets A, B, C…
Projet A : 90000
Projet B : 50000
Projet C : 30000
Projet D : 20000
Etc.
Le capital dont dispose l’entreprise ou la division d’entreprise est limitée à 150000.
Il n’est pas possible de réaliser tous les projets à cause du rationnement du capital.
Quels seront alors les projets à retenir ?
Résolution

|
Projets |
Indice de rentabilité |
Capital nécessaire |
Cumul capital |
Décision |
|
C |
1,05 |
30000 |
30000 |
Oui |
|
A |
1,04 |
90000 |
120000 |
Oui |
|
B |
1,035 |
50000 |
170000 |
Non |
|
D |
1,02 |
20000 |
190000 |
Non |
- Le capital disponible 150000 est dépassé à partir du projet B.
- Les VAN des deux (2) projets retenus totalisent 3600 + 1500 = 5100
- remarquons que le projet D pourrait être réalisé sans que la limite des 150000 soit atteinte
- les VAN des projets retenus totaliseraient VANC + VANA + VAND = 3600 + 1500 + 1400 = 6500
b) La programmation linéaire
Désignons par les variables xa, xb xc xd , les programmes des projets A, B, C, D. Ces variables prennent la valeur de 1 si le programme est réalisé et la valeur de 0 si le programme est refusé.
L’objectif du promoteur est de maximiser la somme des VAN sous contrainte de son budget.
Max : VANxa + VANxb + VANxc + VANxd
Sous contrainte : I0xa + I0xb + I0xc + I0xd ≤ 150000
Max : 3600xa + 1750xb + 1500xc + 400xd
Sous contrainte : 90000xa + 50000xb + 30000xc + 20000xd ≤ 150000
La solution optimale du système est :
xa = 1
xb = 1
xc = 0,33
xd = 0
Les projets A et B et ⅓C sont retenus. Ainsi les VAN des projets retenus totalisent :
VAN(A + B + ⅓C) = [3600 + 1750 + ⅓ (1500)] =
VAN(A + B + ⅓C) = 5850
2 ANALYSE à PARTIR TRI
PROJETS DE MEME TAILLE
Le critère du TRI le plus élevé est souvent utilisé pour sélectionner un des deux projets alternatif. L’usage de ce critère demande cependant des précautions.
Considérons deux projets d’investissement A et B de 90000 chacun et d’une durée de cinq (5) ans. Le coût du capital est de 10%.
Les flux net de liquidité sont indiqués ci après ainsi que leurs VAN au taux de 10%, ainsi que les TRI des projets respectivement :
|
Années Projets |
0 |
1 |
2 |
3 |
4 |
5 |
TRI |
VAN10% |
|
Projet A |
- 90000 |
80000 |
50000 |
20000 |
5000 |
5000 |
42,23% |
45596 |
|
Projet B |
- 90000 |
5000 |
5000 |
40000 |
80000 |
100000 |
26,12% |
65463 |
Selon les critères de la VAN le projet B est préférable.
Alors que selon le critère du TRI c’est le projet A qui est le plus rentable.
Etudions cette contradiction en utilisant le choix de l’investissement le plus utile.
Le critère de choix reposant sur la maximisation de la rentabilité de l’investissement est relativement limité du point de vue de l’entreprise. Il présente deux (2) inconvénients majeurs liés à l’existence possible d’un taux d’indifférence et de la prise en compte du risque.
2.1 Le Problème du taux d'indifférence
Supposant que l’on représente graphiquement les diverses VAN des deux (2) projets A et B en fonctions des divers taux d’actualisation possible :
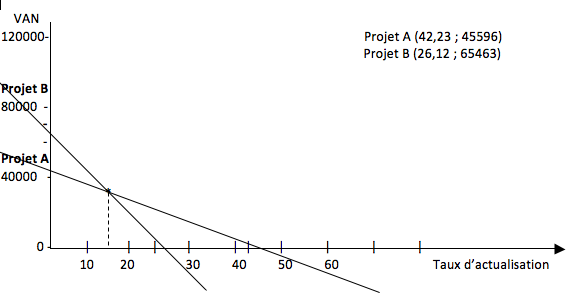
Le taux d’indifférence noté par i* est le taux d’actualisation qui égalise les Van des deux (2) investissements.
Si nous comparons la rentabilité des deux (2) projets en utilisant le critère du TRI c’est le projet A qui sera préféré au projet B car TRIA ≥ TRIB.
Si on choisi la VAN comme critère de comparaisons tout dépendra du taux d’actualisation effectivement utilisé :
- si le coût du capital est ≥ 16,5% (i*) le projet A est plus rentable que le projet B
- si le coût du capital est ≤ 16,5% (i*) le projet B est plus rentable que le projet A
- si le taux du capital est = 16,5% il y a donc une contradiction dans le cas où le coût du capital est ≤ au taux d’indifférence.
Lorsqu’il existe un taux d’indifférence le critère de choix de « rentabilité maximale », ne peut pas être utilisé, parce que rien n’autorise à privilégier la VAN ou le TRI.
2.2 Le Problème du Risque
La comparaison de deux (2) projets selon le critère de la rentabilité maximale peut entrer en contradiction avec la notion de risque lié à un projet. Par rapport au risque et à la rentabilité il faut utiliser deux (2) critères : l’écart type de la VAN (mesure du risque), et l’espérance mathématique de la VAN (mesure de la rentabilité).
La VAN est alors une variable aléatoire.
Le promoteur du projet peut avoir à choisir entre un projet présentant une espérance de gain forte en même temps qu’un risque élevé. Et, un autre projet avec une espérance de gain faible mais associé à un risque modeste. Il lui est alors impossible de choisir de manière purement scientifique tout va dépendre d’une série de jugements subjectifs portés par le promoteur en fonction de ses besoins financiers, de son goût poule risque ou de sa prudence…
Pour contourner la difficulté d’un choix uniquement fondé sur la rentabilité maximale certains experts suggèrent de lui substituer le choix en fonction du critère d’utilité.
La notion d’utilité englobe en fait celle des rentabilités tout en étant plus généralistes. Le profit ne constitue que l’un des objectifs de l’entrepreneur. A côté de cet objectif apparaîtrait par exemple l’objectif de sécurité. Etant donné que le classement ne concerne que les investissements rentables l’entrepreneur peut négliger l’aspect rentabilité. Ainsi l’investissement qui sera choisi sera celui permettant de réaliser au mieux un objectif jugé prioritaire.
En général ces objectifs sont extrêmement nombreux.
Supposant qu’une entreprise peut choisir entre divers projet se soit fixé comme objectif :
- une croissance du chiffre d’affaire de 10%
- un taux de rentabilité des fonds propres de 8%
- l’amélioration de l’image de marque de l’entreprise
- l’amélioration du climat social
- l’amélioration de la qualité du produit.
Il apparaît immédiatement que si certains objectifs sont mesurables d’autres ne le sont pas.
Dans une première étape le choix de l’investissement le plus utile va consister à attribuer à chacun des objectifs un indice permettant de le situer dans une échelle de valeur. Cet indice doit être compris entre 1 et 10.
10 : objectif très important
1 : objectif peu important
En faisant la somme des indices, l’indice attribué à chaque objectif peut alors être transformé en pourcentage. Ce pourcentage indique l’importance relative que le promoteur attache à l’objectif.
Lorsqu’il doit choisir entre plusieurs projets, le promoteur doit évaluer l’impact de chacun sur chaque objectif.
Dans une deuxième étape chaque projet se verra affecté une note moyenne. Calculez en utilisant d’une part ces impacts sur les objectifs et d’autre part les coefficients de pondération affectée à chaque objectif.
Le projet sélectionné sera celui ayant la moyenne la plus forte.
2.3 Arbitrage Entre Espérance Mathématique et Variance
Considérons les projets suivants dont on connaît l’espérance de la VAN et la variance de la VAN
|
Projet |
Espérance VAN |
Variance VAN |
|
A |
12000 |
900000 |
|
B |
15000 |
7840000 |
|
C |
17000 |
8410000 |
E(A) < E(B) < E(C) donc A est le plus rentable
V(A) > V(B) > V(C) donc A est le plus risqué
Ainsi A est le moins rentable et le plus risqué =====> on élimine le projet A. Il ne sera jamais préféré parmi les trois projets.
E(C) > E(B) ======> C est le plus rentable
V(C) > V(B) ======> C est le plus risqué
Cas pratique 2
Un investissement de 80000000 est supposé procurer les CAF d’exploitation suivantes :
|
|
Probabilité |
Année 1 |
Année 2 |
Année 3 |
|
Hypothèse pessimistes |
0,30 |
20000000 |
25000000 |
30000000 |
|
Hypothèse la plus probable |
0,50 |
30000000 |
40000000 |
50000000 |
|
Hypothèse optimiste |
0,20 |
40000000 |
50000000 |
60000000 |
Calculer l’espérance mathématique de la VAN et la variance de la VAN avec un coût du capital de 10%.
Résolution
Avec Hy : Hypothèse
|
Année 1 |
|
Année 2 |
||||||
|
|
Pi |
Ri |
PiRi |
|
Pi |
Ri |
PiRi |
|
|
Hy pessimiste |
0,30 |
20 |
6 |
|
Hy pessimiste |
0,30 |
25 |
7,5 |
|
Hy peu probables |
0,50 |
30 |
15 |
|
Hy peu probables |
0,50 |
40 |
20 |
|
Hy optimiste |
0,20 |
40 |
8 |
|
Hy optimiste |
0,20 |
50 |
10 |
|
Ʃ Pi Ri = 29 |
29 |
Ʃ Pi Ri = 37,5 |
37,5 |
|||||
|
Année 3 |
|
|
||||
|
|
Pi |
Ri |
PiRi |
|
|
|
|
Hy pessimiste |
0,30 |
30 |
9 |
|
||
|
Hy peu probables |
0,50 |
50 |
25 |
|
||
|
Hy optimiste |
0,20 |
60 |
12 |
|
||
|
Ʃ Pi Ri = 46 |
46 |
|
||||
E(X) = Ʃ XiPi
Pi = les probabilités
Xi = les RN
VAN = - I0 + RN1(1+i)-1 + RN2(1+i)-2 + RN3(1+i)-3
VAN = RN1(1+i)-1 + RN2(1+i)-2 + RN3(1+i)-3
E(VAN) = (1+i)-1 E(RN2) + (1+i)-2 E(RN2) + (1+i)-3 E(RN3) = -I0
E(RN1) = (PiRNi)
E(VAN) = 29(1,10)-1 + 37,5(1,10)-2 + 4,6(1,10)-3 – 80
= 11,915
E(VAN) = 11915852
V(RN) = Ʃ PiRi2 – [E(Ri)]2
Supposons que les recettes nettes sont indépendantes les unes des autres avec :
-VAN = (1+i)-1 RN1 + (1+i)-2 RN2 + (1+i)-3 RN3) – I0
V(VAN) = [(1+i)-1]2 V(RN1) + (1+i)-2]2 V(RN2) + [(1+i)-3]2 V(RN3)
V(VAN) = (1+i)-2 V(RN1) + (1+i)-4 V(RN2) + (1+i)-6 V(RN3)
V(RN1) = Ʃ PiRi2 – [E(RNi)]2
|
Année 1 |
|
Année 2 |
||||||
|
|
Pi |
Ri |
PiRi2 |
|
Pi |
Ri |
PiRi2 |
|
|
Hy pessimiste |
0,30 |
20 |
120 |
|
Hy pessimiste |
0,30 |
25 |
187,5 |
|
Hy peu probables |
0,50 |
30 |
450 |
|
Hy peu probables |
0,50 |
40 |
800 |
|
Hy optimiste |
0,20 |
40 |
320 |
|
Hy optimiste |
0,20 |
50 |
500 |
|
Ʃ Pi Ri2 = 890 |
890 |
Ʃ Pi Ri2 = 1487,5 |
1487,5 |
|||||
V(RN1) = ƩPiRi2 – [E(RN1)]2 = 890 - 222 = 49 V(RN2) = ƩPiRi2 – [E(RN2)]2 = 1487,5 – (37,5)2 = 81,25
|
Année 3 |
|
|||||
|
|
Pi |
Ri |
PiRi2 |
|
|
|
|
Hy pessimiste |
0,30 |
30 |
270 |
|
||
|
Hy peu probables |
0,50 |
50 |
1250 |
|
||
|
Hy optimiste |
0,20 |
60 |
720 |
|
||
|
Ʃ Pi Ri2 = 2240 |
2240 |
|
||||
V(RN3) = ƩPiRi2 – [E(RN3)]2 = 2240 – (46)2 = 124
V(VAN) = (1+i)-2 V(RN1) + (1+i)-4 V(RN2) + (1+i)-6 V(RN3)
V(VAN) = 49(1,10)-2 81,25(1,10)-4 +124(1,10)-6
V(VAN) = 165,985
V(VAN) = 166
Remarque
Pour comparer le risque de deux projets, il est pertinent de calculer l’écart réduit défini par :

L’écart réduit de la VAN est parfois appelé coefficient de variation de la VAN.