Utilité et préférences du consommateur
2 La Fonction d'utilité
Soit U la fonction d'utilité et X un panier de biens. L'utilité du panier X sera noté U(X).
La fonction d'utilité permet donc de traduire algébriquement les préférences du consommateur. Une fonction d'utilité associe à chaque panier X un nombre positif appelé "Utilité" du panier.
Pour deux paniers X et Y, on aura les équivalence suivantes :
X = Y si et seulement si U(X) = U(Y)
et X > Y si et seulement si U(X) > U(Y)
U(X) dépend des quantités de bien 1 (x1) et de bien 2 (x2) qui sont les arguments de la fonction U.
![]()
Exemples de fonction d'utilité du consommateur
Les fonctions d'utilités de type Cobb-Douglas représentent des préférences normales de paniers où les biens sont substituables.
![]()
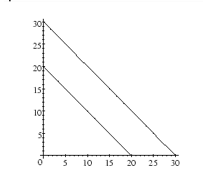
Dans le cas des biens parfaitement substituables, les fonctions d'utilités sont représentées sous forme de droites décroissantes et parallèles.
![]()
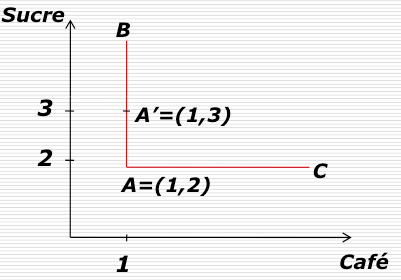
Dans le cas des biens parfaitement complémentaires, les fonctions d'utilités sont représentées sous forme de droites coudées
![]()
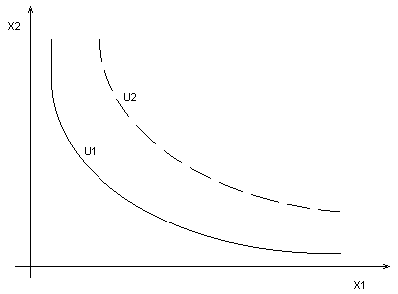
Fonction d'utilité et courbes d'indifférence
Une fonction d'utilité est représentée graphiquement par des courbes d'indifférence. Une courbe d'indifférence C0 représente les paniers qui procurent au consommateur un même niveau d'utilité U0 (U0 est une constant).
L'équation d'une courbe d'indifférence C0 de niveau d'utilité U0 est
![]()
Fonction d'utilité et Utilité marginale
L'utilité marginale du bien 1 est le taux de variation de l'utilité totale lorsqu'un individu qui consomme un panier (x1, x2) de bien reçoit un peu plus de bien 1 (ie Δx1).
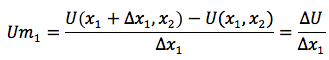
si les variations sont infinitésimales, le calcul des utilités marginales des biens 1 et 2 passe par le calcul des dérivées partielles par rapport à x1 et à x2.
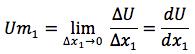
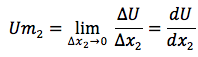
Fonction d'utilité et TMS
Long d'une même courbe d'indifférence, le niveau d'utilité est constant (dU = 0) d'où
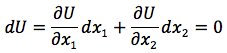
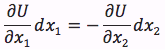
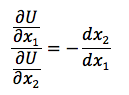
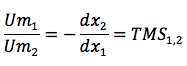
Le TMS est égal au rapport des utilités marginales respectives des biens 1 et 2.